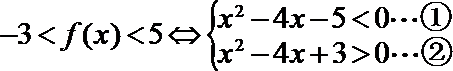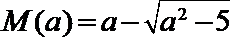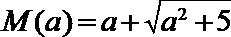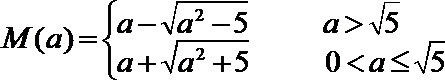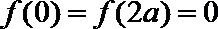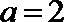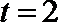- 简单的线性规划
- 共504题
14.若不等式

正确答案
a≥1
解析
解析已在路上飞奔,马上就到!
知识点
22.对于函数








(1)判断函数
(2)已知







(3)在(2)的条件下,试比较

正确答案
(1)
∴
∴ 是“幅度函数”,其“幅度”为2
(2)
∵ 


∴ 当
当
∴ 
∴
(3)
令

∴
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
20.已知


(1)若

(2)求证:对任意

正确答案
(1)依题意





所以
解得
(2)
设
则
考虑到
所以
又当

从而

所以对任意

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数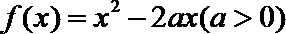
(1)当
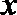
(2)对于给定的正数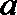



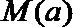
(3)函数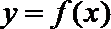
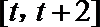

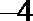
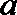
正确答案
(1)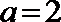
由①得,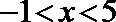
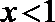
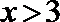
∴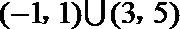
(2)∵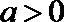
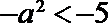
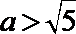
当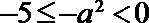
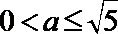
∴
(3)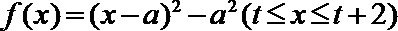
①若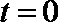
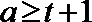
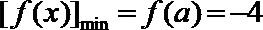
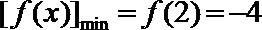
当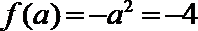
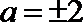
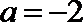
当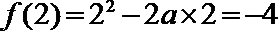
②若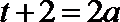
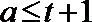
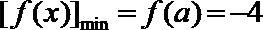
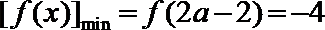
当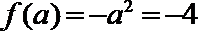
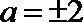
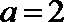
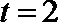
若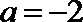
当
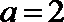
综上所述,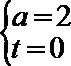
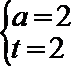
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)设

(2)关于





(3)证明:当




正确答案
(1)函数定义域




(2)







即




(3)

以下证明,对


不等式
反之,由

因为


这说明
这样,不等式
即
∴ 

解析
解析已在路上飞奔,马上就到!
知识点
20.设二次函数



(1)求函数
(2)若对于任意的


正确答案
(1)设
∵ 

∴
∴
(2)
∴
即
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知不等式



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数
(1)若

(2)当方程

(3)若对于一切


正确答案
(1)由
当

当




所以不等式
(2)由
令
由函数图像知两函数图像在y轴右边只有一个交点时满足题意

由
(3)
当


所以
当
①当


令


所以


所以
所以
②当

即
所以
综上,
解析
解析已在路上飞奔,马上就到!
知识点
17.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若对任何

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析