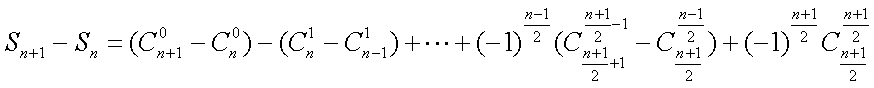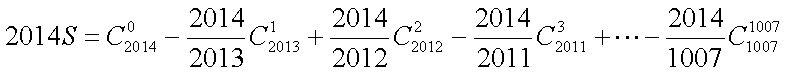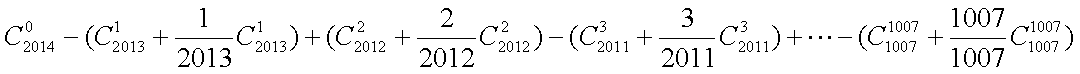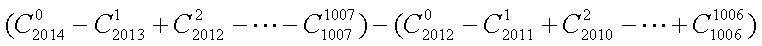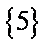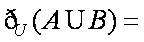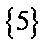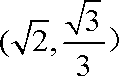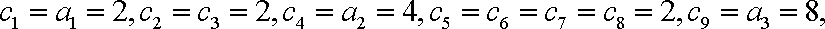- 幂函数的图像
- 共352题
设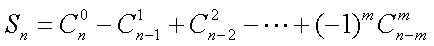
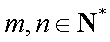
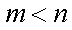
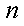
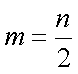
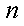
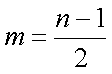
(1)证明:当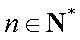

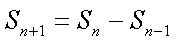
(2)记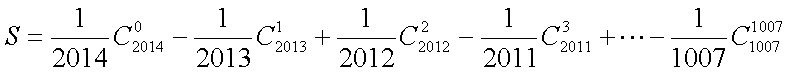
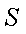
正确答案
见解析。
解析
(1)当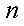
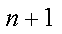
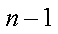
∵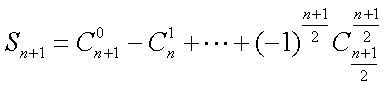
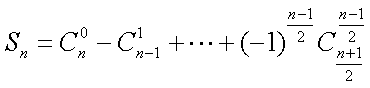
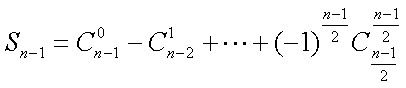
∴
=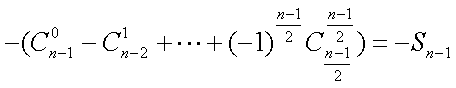
∴当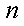
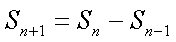
同理可证,当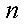
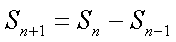
(2)由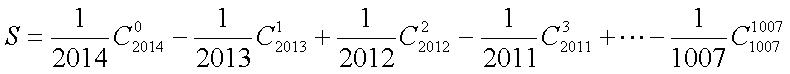
=
=
=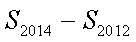
又由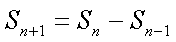
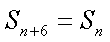
所以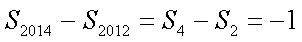
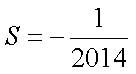
知识点
已知集合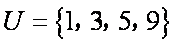
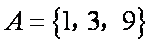
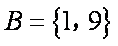
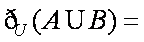
正确答案
解析
易得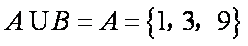
知识点
假设在5秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为
正确答案
解析
设两条短信分别在时刻x、y进人手机,则0<x<5,0<y<5,“手机受到干扰”就是“|x-y|<2”在直角坐标系中,作出点P(x,y)所在区域(如右图).由几何概型知,手机受到干扰的概率为
知识点
设函数
(1)当

(2)证明:对

(3)若


正确答案
见解析
解析
(1)


则


当



当



所以 


(2)因为 

所以当




(3)(证法一)数学归纳法
ⅰ)当
ⅱ)假设当
即若

当





设
由(2)得
=
=
由假设可得 
所以当 
由ⅰ),ⅱ)可知,对一切正整数n∈N*,命题都成立,
所以 若


(证法二)若
那么由(2)可得

知识点
已知矩阵







正确答案
见解析。
解析
由题意知,

所以

所以

知识点
设函数
(1)求函数
(2)设




(3)若



正确答案
见解析
解析
解析:(1)因为

解得:



由


所以

因为
所以函数

(2)由(1)知,当

“对任意








因为
① 当


② 当




所以
③ 当









令







所以
综上所述,若对任意


则实数

(3)证明:由(1)知,当


当






所以
又因为
所以



当且仅当
知识点
如果存在常数







(1)若数列:



(2)已知有穷等差数列





(3)对于一个不少于3项,且各项皆为正整数的递增数列
正确答案
见解析
解析
(1)因为数列:

所以

故
即
(2)设数列



若
即对数列

同理可得:若

由“兑换数列”的定义可知,数列

又因为数列



(3)假设存在这样的等比数列

因为数列
则
又因为数列


故数列

则
①若




②若

即


综合①②得,不存在满足条件的数列
知识点
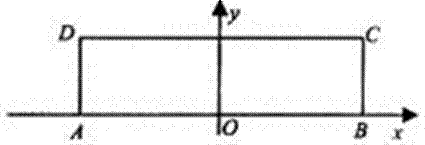
已知长方形ABCD,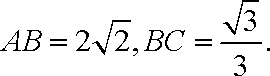

(1)求以A,B为焦点,且过C,D两点的椭圆P的标准方程;
(2)已知定点E(—1,0),直线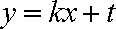

正确答案
见解析。
解析
(1)由题意可得点A,B,C的坐标分别为
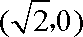
设椭圆的标准方程是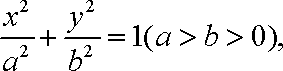
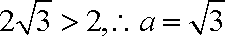
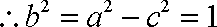
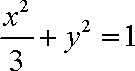
(2)将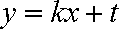
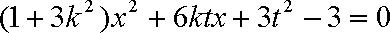
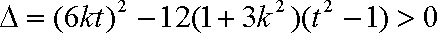
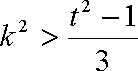
设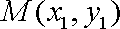
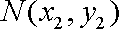
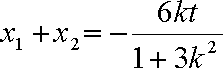
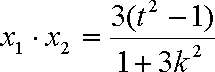
因为以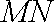

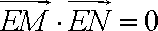
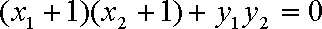
而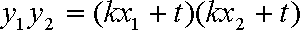
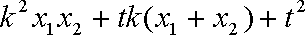
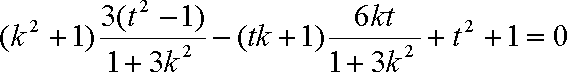
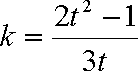
如果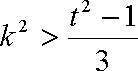

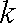
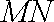

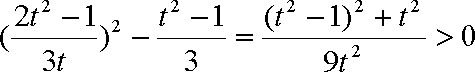
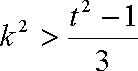

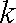
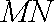

知识点
已知矩阵


正确答案
见解析。
解析
矩阵M的特征多项式为
令


令

知识点
已知数列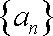
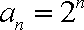
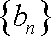
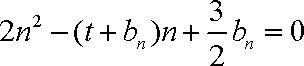
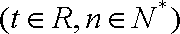
(1)试确定实数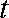
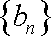
(2)当数列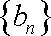
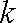
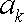
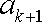
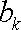
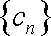
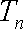

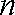
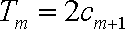
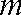
正确答案
见解析
解析
(1)当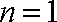
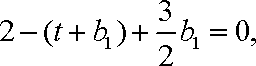
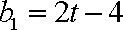
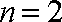
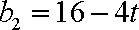

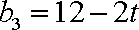
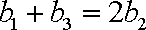
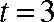
而当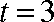
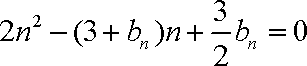
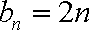
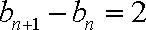
故此时数列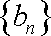
(2)由题意知,
则当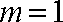
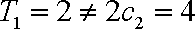
当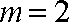
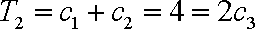
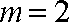
当
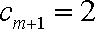
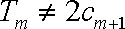
从而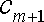
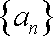
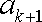

b1个 b2个 b3个 bk个
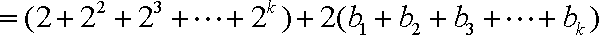
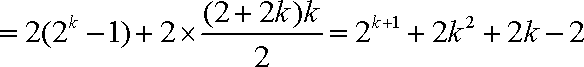
又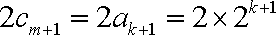
所以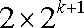
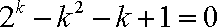
所以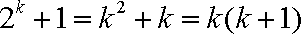
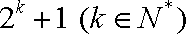
而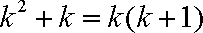
即当
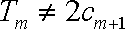
知识点
扫码查看完整答案与解析