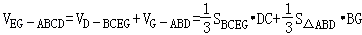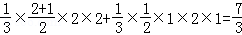- 幂函数的图像
- 共352题
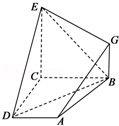
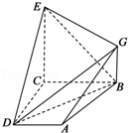
17.如图，已知四边形ABCD和BCEG均为直角梯形，AD∥BC，CE∥BG，且∠BCD=∠BCE=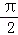
（1）EC⊥CD；
（2）求证：AG∥平面BDE；
（3）求：几何体EG﹣ABCD的体积．
正确答案
见解析。
解析
（1）证明：由平面ABCD⊥平面BCEG，
平面ABCD∩平面BCEG=BC，CE⊥BC，CE⊂平面BCEG，
∴EC⊥平面ABCD，
又CD⊂平面BCDA，故EC⊥CD
（2）证明：在平面BCEG中，过G作GN⊥CE交BE于M，连DM，
则由已知知；MG=MN，MN∥BC∥DA，且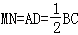
∴MG∥AD，MG=AD，故四边形ADMG为平行四边形，∴AG∥DM
∵DM⊂平面BDE，AG⊄平面BDE，∴AG∥平面BDE
（3）解：
=
知识点
16.已知函数
（1）求
（2）若
正确答案
见解析。
解析
（1）
（2）
知识点
已知函数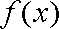
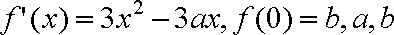
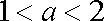
（1）若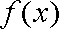
（2）在（1）的条件下，求经过点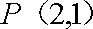
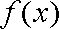
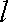
（3）设函数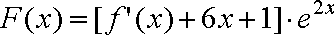
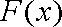
正确答案
见解析
解析
解析：（1）由已知得，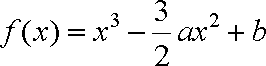
由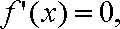
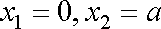
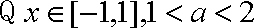
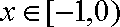
当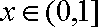
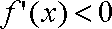
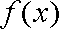
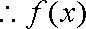
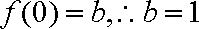
又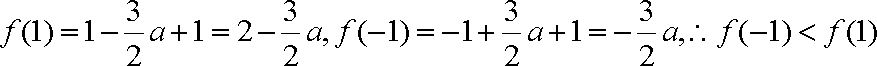
由题意得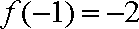
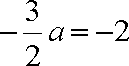
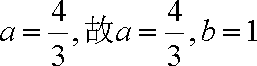
（2）解：由（1）得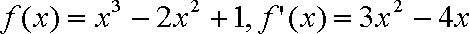
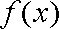
①当切点为P（2，1）时，切线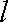
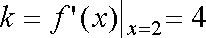
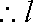
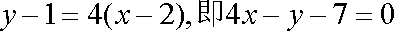
②当切点P不是切点时，设切点为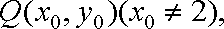
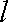
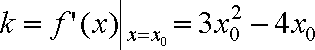
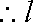
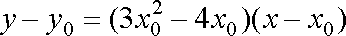
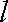
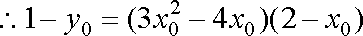
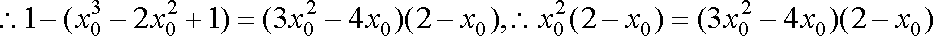
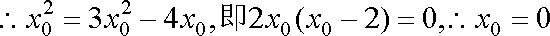
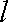
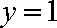
故所求切线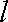
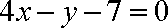
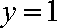
（3）解：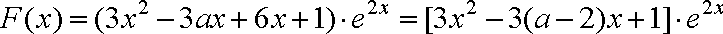
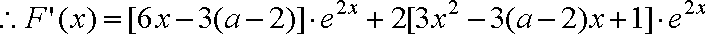
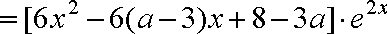
二次函数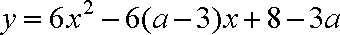
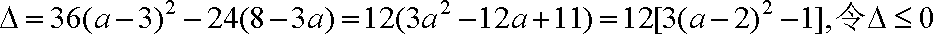
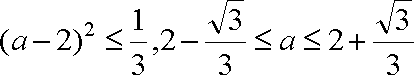
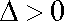
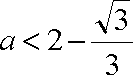
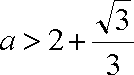
因为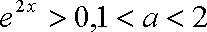
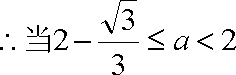
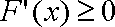
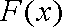
当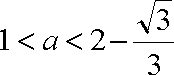
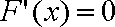
可知函数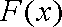
知识点
已知集合A={x｜x2＋x－2<0｝，集合B= {x｜(x＋2) (3－x)＞0｝，则
正确答案
解析
∵A＝{x|－2＜x＜1}，B＝{x|－2＜x＜3}，∴(
知识点
2.已知函数①y=sinx+cosx，②y=
A两个函数的图象均关于点(-
B两个函数的图象均关于直线x=-
C两个函数在区间(-
D两个函数的最小正周期相同
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
21．已知
（1）若
（2）求
（3）设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12.设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．向量
A向左平移
B向右平移
C向左平移
D向右平移
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知函数
（1）求
（2）若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
22．设
（Ⅰ）求证：
（Ⅱ）求证： 
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析