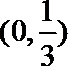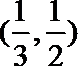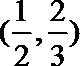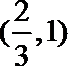- 幂函数的图像
- 共352题
20.已知函数

(1)当


(2)如果函数









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数

(Ⅰ)当

(Ⅱ) 当




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若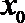
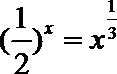
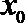
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.在复平面内,复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.(考生注意:请在下列二题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(1)(几何证明)
选如图,A,E是半圆周上的两个三等分 点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为___________.
(2)(坐标系与参数方程)
在已知极坐标系中,已知圆


正确答案
(1)
(2)2或-8
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数


(1)若


(2)求证:当


(3)若对任意的



正确答案
解:( 1)由已知,得 




(3)



于是问题等价于:对任意的

记

则










若


在此区间上,有 


这时,







解析
解析已在路上飞奔,马上就到!
知识点
17.若


(1)求

(2)⊿ABC中a、b、c分别是∠A、∠B、∠C的对边。若

正确答案
解:(1)

由题意,函数



所以,
(2)∵(

∴

⊿ABC中, 则由正弦定理得:



解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.数列




正确答案
49
解析
解析已在路上飞奔,马上就到!
知识点
请从22~24三题中任选一题作答。
22.选修4—1:几何证明选讲
如图,⊙














证明:(1)
(2)
正确答案
22.
证明:(1)因为


又



由①②得
(2)连接






所以




23.解:(1)


24.解:(Ⅰ)

(Ⅱ)
函数


解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析