- 匀变速直线运动规律的综合运用
- 共190题
14.交通信号“绿波”控制系统一般被称为“绿波带”,它是根据车辆运行情况对各路口红绿灯进行协调,使车辆通过时能连续获得一路绿灯。郑州市中原路上某直线路段每间隔L=500 m就有一个红绿灯路口,绿灯时间△t1=60 s,红灯时间△t2=40 s,而且下一路口红绿灯亮起总比当前路口红绿灯滞后△t=50s。要求汽车在下一路口绿灯再次亮起后能通过该路口。汽车可看做质点,不计通过路口的时间,道路通行顺畅。
(1)若某路口绿灯刚亮起时,某汽车恰好通过,要使该汽车保持匀速行驶,在后面道路上再连续通过五个路口,满足题设条件下,汽车匀速行驶的最大速度是多少?最小速度又是多少?(计算结果保留两位有效数字)
(2)若某路口遭遇红灯,待绿灯刚亮起时,某汽车由静止开始,以加速度a=2 m/s2匀加速运动,加速到第(1)问中汽车匀速行驶的最大速度以后,便以此速度一直匀速运动。试通过计算判断,当该汽车到达下一个路口时能否遇到绿灯。
正确答案
(1)
(2)走到下个路口时能够遇到绿灯
解析
(1)若汽车刚好在绿灯亮起时通过第五个路口,则通过五个路口的时间
此时匀速运动的速度最大
若汽车刚好在绿灯熄灭时通过第五个路口,则通过五个路口的时间
此时匀速运动的速度最小
(2)若路口绿灯刚亮起时,汽车启动加速,最终加速到

在此过程中汽车走过的位移 
然后汽车以此速度匀速运动,可知

因此,汽车从该路口开始启动到下一个路口的时间为
110 s>t>50 s,因此走到下个路口时能够遇到绿灯。
考查方向
多过程的匀速直线运动和匀变速直线运动的分析求解。
解题思路
连续通过五个路口的最大行驶速度,是第五个路口绿灯亮起时汽车刚好通过第五个路口;连续通过五个路口的最小行驶速度,是第五个路口绿灯熄灭起时汽车刚好通过第五个路口;对于(2),可通过比较汽车到达下一个路口的时间与从第一个路口绿灯亮起到第二个路口绿灯亮起的时间,来判断是否能通过下一个路口。
易错点
题干中的时间就有三个,即△t1,△t2和△t,很容易干扰学生的思考过程,导致分析不清汽车的运动情况;
知识点
(10分)如图所示,粗糙斜面与光滑水平面通过可忽略的光滑小圆弧平滑连接,斜面倾角α=370.A、B是两个质量均为m=1kg的小滑块(可视为质点),C为左侧附有胶泥的竖直薄板(质量均不计),D是两端分别水平连接B和C的轻质弹簧.当滑块A置于斜面上且受到大小F=4N、方向垂直斜面向下的恒力作用时,恰能沿斜面向下匀速运动.现撤去F,让滑块A从斜面上距底端L=1m处由静止下滑,求:(g=10m/s2,sin370=0.6)
27.滑块A到达斜面底端时的速度大小;
28.滑块A与C接触粘在一起后,A、B和弹簧构成的系统在作用过程中,弹簧的最大弹性势能.
正确答案
①(5分)
解析
①设




考查方向
动能定理
解题思路
应用平衡条件与动能定理可以求出到达斜面底端的速度.
易错点
关键能正确表示出合外力做的总功.
教师点评
本题考查了动能定理,在近几年的各省高考题出现的频率较高,常与匀变速直线运动规律的综合运用等知识点交汇命题.
正确答案
②(5分)
解析
②当A、B具有共同速度时,系统动能最小,弹簧的弹性势能最大,为
则,
联立以上两式解得:
考查方向
功能关系;动量守恒定律
解题思路
当A、B具有共同速度时,系统动能最小,弹簧的弹性势能最大,根据动量守恒定律与动能定理求解.
易错点
关键通过分析知道当A、B具有共同速度时,弹簧的弹性势能最大.
教师点评
本题考查了功能关系,动量守恒定律,在近几年的各省高考题出现的频率较高,常与功的计算、动能定理等知识点交汇命题.
如图所示,一长L=2m、质量M=4kg的薄木板(厚度不计)静止在粗糙的水平台面上,其右端距平台边缘l= 5m,木板的正中央放有一质量为m=1kg的小物块(可视为质点),已知木板与地面

27.F作用了1.2s时,木板的右端离平台边缘的距离;
28.要使小物块最终不能从平台上滑出去,则物块与平台间的动摩擦因数
正确答案
0.64m
解析
假设开始时物块与木板会相对滑动,由牛顿第二定律:
对木板:

对物块:

设作用t秒后,小物块恰好从木板左端滑离,则
,解得
在此过程:木板位移
物块位移

在小物块从木板上滑落后的0.2s内,由牛顿第二定律:
对木板:

木板发生的位移
此时木板距平台边缘
考查方向
牛顿第二定律;匀变速直线运动的公式
解题思路
先假设F作用下物块与木板相对滑动,作用的过程中分别对物块和木板受力分析,使用牛顿运动定律列出式子,解得木块、物块的加速度,最后验证假设是否成立;分别考虑物块在木板上运动与物块滑下木板后的运动情况,结合运动规律及牛顿定律列式可以求出木板距平台边缘的距离.
易错点
关键根据牛顿第二定律求出木板与小物块的加速度,判断两者是否相对滑动.
教师点评
本题考查了牛顿第二定律;匀变速直线运动的公式,在近几年的各省高考题出现的频率较高,常与动能定理等知识点交汇命题.
正确答案
解析
小物块滑至平台后,做匀减速直线运动,由牛顿第二定律:
对物块:



联立解得
考查方向
牛顿第二定律;匀变速直线运动的公式
解题思路
物块在平台上运动,受平台对物块的摩擦力作用做匀减速运动,要使物块不滑下平台,则物块滑下木板后在平台上减速运动到速度为零时依然在平台上,临界点是物块运动到平台的最右端时,速度恰好为零。结合运动学规律及牛顿定律可以求解.
易错点
关键由几何关系分析出木板不会从平台上掉下去的条件.
教师点评
本题考查了牛顿第二定律;匀变速直线运动的公式,在近几年的各省高考题出现的频率较高,常与动能定理、匀变速直线运动的图像等知识点交汇命题.
27.质量M=3kg的滑板A置于粗糙的水平地面上,A与地面的动摩擦因数µ1=0.3,其上表面右侧光滑段长度L1=2m,左侧粗糙段长度为L2,质量m=2kg、可视为质点的滑块B静止在滑板上的右端,滑块与粗糙段的动摩擦因数µ2=0.15,取g=10m/s2,现用F=18N的水平恒力拉动A向右运动,当A、B分离时,B对地的速度vB=1m/s,求L2的值。
正确答案
.解:
在F的作用下,A做匀加速运动,B静止不动,当A运动位移为L1时B进入粗糙段,设此时A的速度为vA,则:
对A:由动能定理: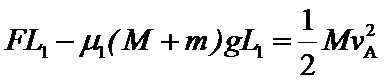
B进入粗糙段后,设A加速度为aA,B加速度为aB,
对A:由牛顿第二定律: 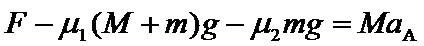
对B:由牛顿第二定律: 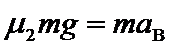
由①得vA=2m/s④ 由②得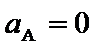
即A以vA=2m/s的速度做匀速直线运动直至A、B分离,设分离时B的速度为vB,B在粗糙段滑行的时间为t,则:
对A: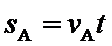
对B: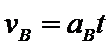
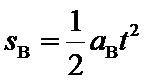
又: 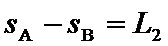
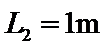
评分:①②每式2分,③④⑤⑥⑦⑧⑨⑩每式1分
(①式用牛顿运动定律求解也行;②式直接写成F=f也行。其它方法正确照样给分)
解析
.解:
在F的作用下,A做匀加速运动,B静止不动,当A运动位移为L1时B进入粗糙段,设此时A的速度为vA,则:
对A:由动能定理: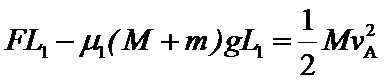
B进入粗糙段后,设A加速度为aA,B加速度为aB,
对A:由牛顿第二定律: 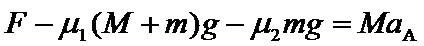
对B:由牛顿第二定律: 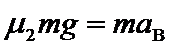
由①得vA=2m/s④ 由②得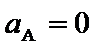
即A以vA=2m/s的速度做匀速直线运动直至A、B分离,设分离时B的速度为vB,B在粗糙段滑行的时间为t,则:
对A: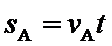
对B: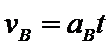
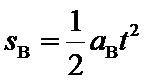
又: 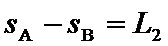
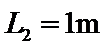
评分:①②每式2分,③④⑤⑥⑦⑧⑨⑩每式1分
(①式用牛顿运动定律求解也行;②式直接写成F=f也行。其它方法正确照样给分)
考查方向
摩擦力,牛顿第二定律。
解题思路
由牛顿第二定律分析物理过程,再由几何关系分析s,t,v过程,最后用动能定理求解。
易错点
过程的把握不清晰
教师点评
此题较好的考察了 牛顿第二定律和动能定理的过程分析,在平时训练时应注意对解题思路的三步分析。
知识点
在静止的液体中下落的物体受到的阻力与速度成正比,即



28.求乙球刚进入水面时的加速度;
29.若将甲乙两球均由紧贴水面处先后由静止释放,释放的时间间隔为
30.下落过程中,若乙球恰能追上甲球,追上时甲球下落的高度为H,追上之前乙球一直做减速运动,求该过程乙球克服水的阻力做的功;
正确答案
(1)根据自由落体运动,则乙球刚进入水面时速度为:


正确答案
(2)根据题意可以知道,当二者都达到收尾速度的时候,二者之间的距离最大,故:



正确答案
(3)根据题意,乙球恰好追上甲球,说明追上时,乙球的速度达到收尾速度
则对乙球根据动能定理:
解析
考查方向
动能定理的运用,牛顿第二定理。
解题思路
教师点评
理解收尾速度,明确运动状态,列好题目方程,综合运用动能定理分析,难度适中。
扫码查看完整答案与解析



















