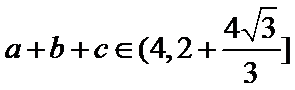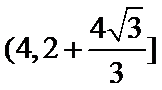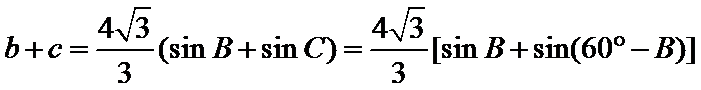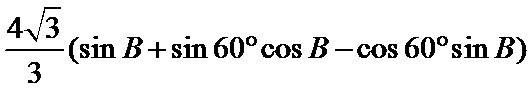余弦定理
共145题

· 余弦定理

余弦定理
共145题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 12 分

已知的内角的对边分别为，且满足.

17.求的值；

18.若，求的面积.

第(1)小题正确答案及相关解析

正确答案

；

解析

∵，∴，

∴，∴，∴，∴，∴.

考查方向

本题主要考查了三角恒等变换，正余弦定理，以及三角形面积。

解题思路

第一问中用两角和差公式和三角恒等变换化简得到，再由正弦定理可得；

易错点

第一问中想不到将角拆成；

第(2)小题正确答案及相关解析

正确答案

解析

∵，，∴，∴，∴.

∴，即的面积的.

考查方向

本题主要考查了三角恒等变换，正余弦定理，以及三角形面积。

解题思路

第二问中用倍余弦定理得到一个角，在用三角形面积公式求得面积。

易错点

第二问中用余弦定理求角时容易将特殊角记错。

题型：简答题

简答题 · 12 分

在△ABC中，已知a，b, c分别是角A，B，C的对边，且满足．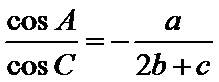

17.求角A的大小;

18.若a=2，求△ABC的周长的取值范围．

第(1)小题正确答案及相关解析

正确答案

（1）；

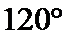
解析

（1）由正弦定理，得，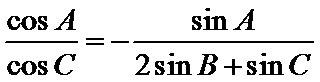

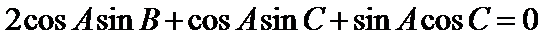
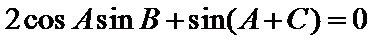
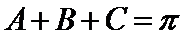
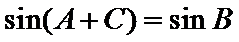
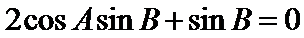
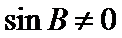
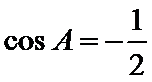
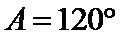
∴，则．

∵，∴，∴．

∵，∴，∴．源:Zxxk.Com]

考查方向

本题主要考查了正弦定理的应用，近几年高考考查频率很高，常考查通过正余定理求角或边等问题。

解题思路

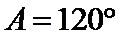
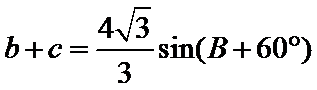
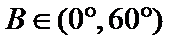
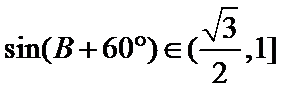
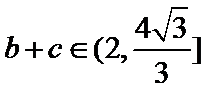
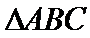
（1）利用已知条件和正弦定理求出角A（2）利用（1）中和a=2及正弦定理表示出，又得到即。故的周长

易错点

通过正弦定理表示三边即周长，易忽视角的范围出错。

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（2）由正弦定理，得，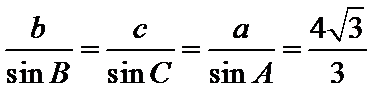

∴

＝

＝．

∵，∴，∴，∴，

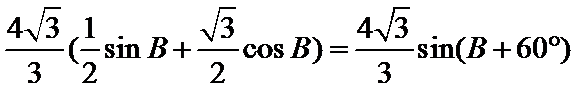
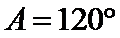
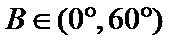
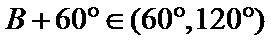
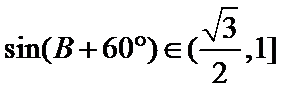
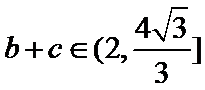
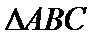
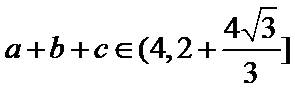
∴，故的周长．

考查方向

本题主要考查了正弦定理的应用，近几年高考考查频率很高，常考查通过正余定理求角或边等问题。

解题思路

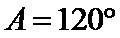
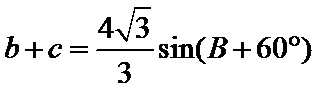
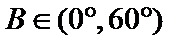
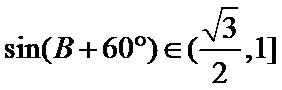
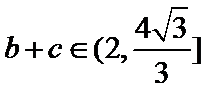
（1）利用已知条件和正弦定理求出角A（2）利用（1）中和a=2及正弦定理表示出，又得到即。故的周长

易错点

通过正弦定理表示三边即周长，易忽视角的范围出错。

题型：填空题

填空题 · 5 分

5. 在中，，，，则_ _.

正确答案

解析

由正弦定理得，所以，又，所以。

考查方向

本题主要考查利用正余弦定理解三角形，意在考查考生对于正余弦定理的基本理解和运算。

解题思路

1.先利用正弦定理求出角C；2.利用大边对大角求出角C的准确值。

易错点

1.不知道应该用什么定理；2.不会根据大边对大角舍去一个角，导致结果出错。

知识点

正弦定理余弦定理三角形中的几何计算

题型：简答题

简答题 · 12 分

如图，在平面四边形中，，，，，.

17.求；

18.求的长.

第(1)小题正确答案及相关解析

正确答案

(1) ;

解析

（Ⅰ）在中，由余弦定理得：，

即，解得：，或（舍），

由正弦定理得：

考查方向

本题主要考查利用正余弦定理解三角形的知识，意在考查考生的运算求解能力。

解题思路

先利用余弦定理求出，后利用正弦定理求解即可；

易错点

不知道该在哪个三角形中使用什么定理；

第(2)小题正确答案及相关解析

正确答案

;(2)

解析

（Ⅱ）由（Ⅰ）有：，，

所以,

由正弦定理得：

考查方向

本题主要考查利用正余弦定理解三角形的知识，意在考查考生的运算求解能力。

解题思路

利用第（1）问的结论求出，然后利用正弦定理求解即可。

易错点

意识不到是互余的关系导致第（2）问无法正确求解。

题型：简答题

简答题 · 15 分

如图所示，在四边形中， =，且，，．

16.求△的面积；

17.若，求的长．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

（Ⅰ）

因为，所以，

所以△ACD的面积．

考查方向

本题考查余弦定理以及正弦定理的应用，属于中档题．

解题思路

利用已知条件求出∠D角的正弦函数值，然后求的面积；

易错点

主要易错于计算出错，

第(2)小题正确答案及相关解析

正确答案

见解析

解析

（Ⅱ）在△ACD中，，

所以．

在△ABC中，

把已知条件代入并化简得：因为，所以

考查方向

本题考查余弦定理以及正弦定理的应用，属于中档题．

解题思路

利用余弦定理求出AC，通过，利用正弦定理求解AB的长．

易错点

主要易错于计算出错，

继续学习学习下一知识点

下一知识点 : 余弦定理的应用

百度题库 > 高考 > 理科数学 > 余弦定理

扫码查看完整答案与解析