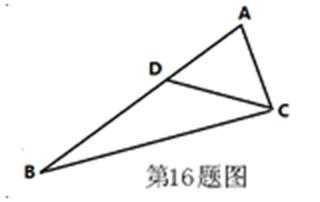
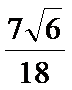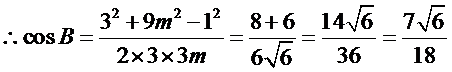- 余弦定理
- 共145题
△ABC中,
17.求BC的长;
18.求△DBC的面积。
正确答案
3
解析
解∵cos∠ABC
在△ABC中,设BC=a,AC=3b ∴9b2=
在△ABD中, cos∠ADB=
在△BDC中, cos∠BDC=
cos∠ADB=-cos∠BDC


由①②
考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
正确答案
解析
解

考查方向
解题思路
利用角的关系,利用余弦定理得到边的关系,通过解方程求得BC长。
易错点
含有a的方程不易处理。
16.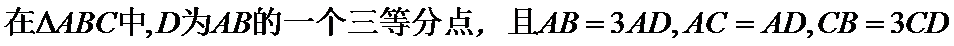
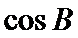
正确答案
解析
令AC=AD=1,CD=x > 0 , 则 AB=3 , BC= 3x ,
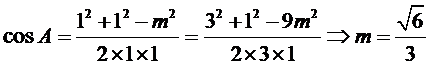
考查方向
解题思路
1.先设出题中需要的线段的长度;
2.根据余弦定理求出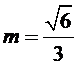
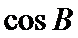
易错点
1.不会设出长度解决问题;
2.不会利用角A的余弦构造方程解方程。
知识点
在△ABC中,已知AB=2,AC=3,A=60°.
17.求BC的长;
18.求sin2C的值.
正确答案
解析
(1)由余弦定理可得:BC2=AB2+AC2﹣2AB•ACcosA=4+8﹣2×2×3×
所以BC=
考查方向
解题思路
直接利用余弦定理求解即可。
易错点
本题考查余弦定理的应用,正弦定理的应用,在计算时易错。
正确答案
解析
由正弦定理可得:



∵AB<BC,∴C为锐角,
则cosC=


因此sin2C=2sinCcosC=2×

考查方向
解题思路
利用正弦定理求出C的正弦函数值,然后利用二倍角公式求解即可.
易错点
本题考查二倍角的三角函数,在限制角的范围过程中易错。
正确答案
知识点
已知函数
17.求函数
18.在




正确答案
解析
(1)由图象知A=1, 
将点


所以
考查方向
解题思路
利用函数的图象,求出A,通过函数的周期求出ω,通过函数的图象经过


易错点
三角函数的解析式中,求的值是难点,熟悉正余弦函数图象是关键.
正确答案
解析
由
所以
因为

所以

所以
考查方向
解题思路
利用

易错点
无
正确答案
LUE
知识点
正确答案
略
知识点
乙是A市的建材经销商,因资金周转困难,便从A市甲处借了50万元人民币,购买了一批建材,并销售给了B市的丙,约定价款为60万元人民币,但丙未付款。乙与丙约定的合同履行地在A市。后来,甲要求乙还钱,乙说因为丙没有支付货款,所以无力偿还。鉴于此,甲欲直接起诉丙,要求其支付50万元。如果甲对丙提起诉讼,法院在下列何种情形下应当受理( )。
A.甲对乙的债权未到期
B.甲向A市的法院起诉
C.乙不愿意通过诉讼或仲裁的方式主张对丙的到期债权
D.甲以乙的名义起诉
正确答案
C
解析
暂无解析
解答题:解答应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)







(Ⅰ) 求
(Ⅱ)若



正确答案
(Ⅰ)


(Ⅱ)因为








解析
解析已在路上飞奔,马上就到!
知识点
已知函数



正确答案
解析
离开家LKS酒店离开加大啊大大大
考查方向
卡结算点开链接阿斯利康的
解题思路
爱是顶顶顶顶顶的顶顶顶顶顶多多多
易错点
是事实上事实上事实上事实上是
教师点评
阿萨的顶顶顶顶顶顶顶顶顶顶顶顶顶顶顶大多多多立刻就撒了肯德基萨拉快点进来看三就了看撒娇的了卡萨就离开的就款了撒娇的理科生就看到了奖励卡检索到立刻就撒了肯德基来看撒娇的离开家萨克雷的就来看撒娇的理科生都流口水了肯定是考虑到看拉手机登了卡结算了肯德基撒立即克拉拉肯德基凯撒蓝就点开了升级打开老师教的款了撒娇的理科生就看到了上考虑绝对是理科开水将打开实际空间萨克的垃圾筐的撒空间的卡卡的萨拉大乐扣乐扣
知识点
扫码查看完整答案与解析