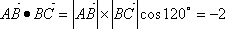余弦定理的应用
共46题

· 余弦定理的应用

余弦定理的应用
共46题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：简答题

简答题 · 14 分

在中，角所对的边分别为a,b,c.

已知且.

（1）当时，求的值；

（2）若角为锐角，求p的取值范围；

正确答案

（1）或（2）

解析

（1）解：由题设并利用正弦定理，得

解得或

（2）解：由余弦定理，b2=a2+c2-2ac cosB

=（a+c）2-2ac cosB

=p2b2-即

因为得，由题设知，所以

知识点

正弦定理的应用余弦定理的应用

题型：填空题

填空题 · 5 分

如图4，是圆的切线，切点为，直线与圆交于

，两点，的平分线分别交弦，于，

两点，已知，，则的值为，

正确答案

解析

略

知识点

余弦定理的应用

题型：单选题

单选题 · 5 分

如图，在中，则 ( )

B-1

D-2

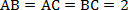
正确答案

解析

本题主要考查向量的数量积的定义

知识点

余弦定理的应用

题型：单选题

单选题 · 5 分

若的内角所对的边满足，且，则的值为

正确答案

解析

由得，由得，解得

知识点

余弦定理的应用

题型：填空题

填空题 · 5 分

已知，，则与的夹角为 .

正确答案

解析

根据已知条件，去括号得：，

知识点

余弦定理的应用

题型：填空题

填空题 · 5 分

设△ABC的内角A，B，C的对边分别为a，b，c，且，则c=（）。

正确答案

解析

∵ A和B都为三角形的内角，且cosA=，cosB=，

∴ sinA==，sinB==，

∴ sinC=sin（A+B）=sinAcosB+cosAsinB=×+×=，

又b=3，

∴ 由正弦定理=得：c===。

知识点

余弦定理的应用

题型：填空题

填空题 · 4 分

在中，角所对的边的长度分别为，且，则　 .

正确答案

解析

略

知识点

余弦定理的应用

题型：简答题

简答题 · 10 分

已知△ABC的三边长都是有理数。

（1）求证cosA是有理数；

（2）求证：对任意正整数n，cosnA是有理数。

正确答案

见解析。

解析

（方法一）（1）证明：设三边长分别为，，∵是有理数，

是有理数，分母为正有理数，又有理数集对于除法的具有封闭性，

∴必为有理数，∴cosA是有理数。

（2）①当时，显然cosA是有理数；

当时，∵，因为cosA是有理数， ∴也是有理数；

②假设当时，结论成立，即coskA、均是有理数。

当时，，

，

解得：

∵cosA，，均是有理数，∴是有理数，

∴是有理数。

即当时，结论成立。

综上所述，对于任意正整数n，cosnA是有理数。

（方法二）证明：（1）由AB、BC、AC为有理数及余弦定理知

是有理数。

（2）用数学归纳法证明cosnA和都是有理数。

①当时，由（1）知是有理数，从而有也是有理数。

②假设当时，和都是有理数。

当时，由，

，

及①和归纳假设，知和都是有理数。

即当时，结论成立。

综合①、②可知，对任意正整数n，cosnA是有理数。

知识点

余弦定理的应用数学归纳法的应用

题型：填空题

填空题 · 5 分

如图3,在中,斜边,直角边,如果以C为圆心的圆与AB相切于,则的半径长为 ▲

正确答案

解析

在Rt△ABC中,∵AB=12,AC=6,即AC=AB,∴∠B=30°,∠A=90°-∠B=60°。

∴CD=AC·sinA=6×

知识点

余弦定理的应用

继续学习学习下一知识点

下一知识点 : 三角形中的几何计算

百度题库 > 高考 > 理科数学 > 余弦定理的应用

扫码查看完整答案与解析