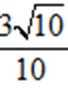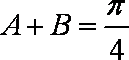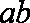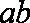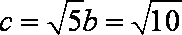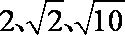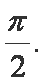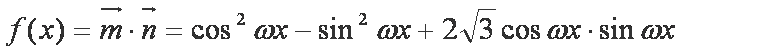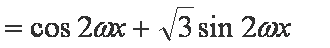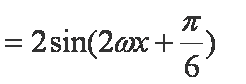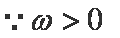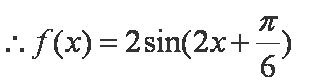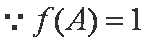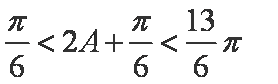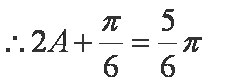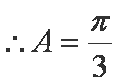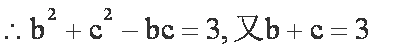- 余弦定理
- 共145题
在△ABC中,角A,B,C的对边分别是a,b,c,满足b2+c2=bc+a2.
(1)求角A的大小;
(2)已知等差数列{an}的公差不为零,若a1cosA=1,且a2,a4,

正确答案
见解析
解析
(1)∵b2+c2-a2=bc, ∴


又A∈(0,π),∴A=
(2)设{an}的公差为d, 由已知得a1=
∴(a1+3d)2=(a1+d)(
∴an=2n. 
∴
∴Sn=(1-






知识点
在ABC中,设角A、B、C所对的边分别为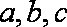
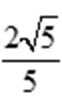
(1)求角C的大小;
(2)若ABC的面积为1,求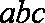
正确答案
(1)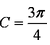
解析
(1)∵
∴ 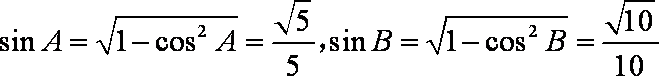
∵ 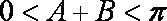
∴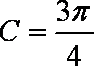
(2)法一:由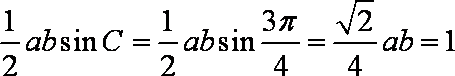
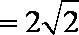
同理得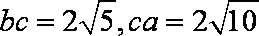
所以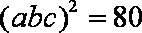
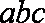
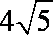
法二:由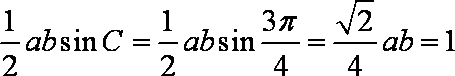

由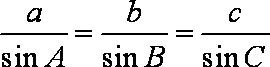
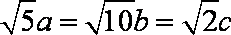
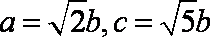
∴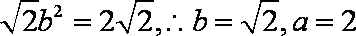
即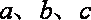
所以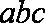
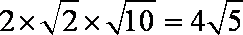
知识点
已知函数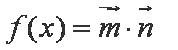
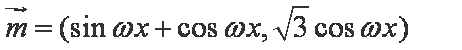
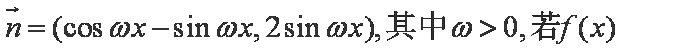
(1)求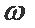
(2)在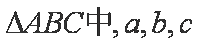
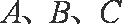
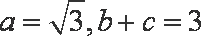
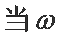
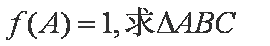
正确答案
见解析
解析
解析:(1)
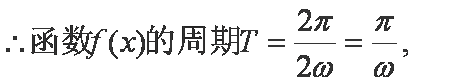
解得
(2)由(1)可知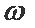

由余弦定理知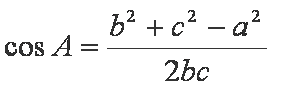
联立解得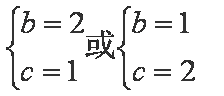
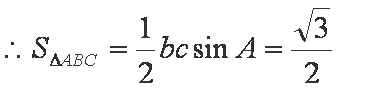
知识点
已ΔABC的内角A,B,C对的边分别为 a,b,c 



(1)求角A的大小;
(2)若a = 1,求b +c的取值范围.
正确答案
(1)
解析
(1)由


再由正弦定理得:
又
所以
又
(2)由正弦定理得


故b+c的取值范围为(1,2] . ……12分
知识点
在△








正确答案
解析
由正弦定理,


知识点
扫码查看完整答案与解析