热门试卷

1 填空题 · 5 分

如图，AB是半圆O的直径，P在AB的延长线上，PD与半圆O相切于点C，AD⊥PD，若PC=4，PB=2，则CD=　　。

1 简答题 · 10 分

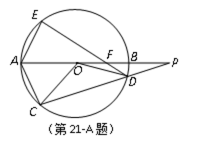
如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC， DE交AB于点F，求证：△PDF∽△POC。

1 简答题 · 7 分

设曲线2x2+2xy+y2=1在矩阵A=（）（a＞0）对应的变换作用下得到的曲线为x2+y2=1。

（1）求实数a，b的值。

（2）求A2的逆矩阵。

1 简答题 · 10 分

如图，AB为O的直径，直线CD与O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直AB于F，连接AE，BE.证明：

（1）∠FEB＝∠CEB；

（2）EF2＝AD·BC.

1 填空题 · 7 分

选修4-2：矩阵与变换

设，若矩阵A＝的变换把直线变换为另一直线。

（1）求的值；

（2）求矩阵A的特征值。

继续学习学习下一知识点

下一知识点 : 平行线等分线段定理

百度题库 > 高考 > 理科数学 > 平行截割定理

扫码查看完整答案与解析