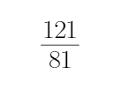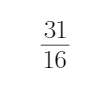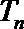- 等比数列的性质及应用
- 共180题
13．各项均为正数的等比数列{an}的前n项和为Sn，a1=1，a2•a4=16则S4=_________
正确答案
15
解析
解析已在路上飞奔，马上就到！
知识点
11．受2008年国际金融危机的影响，某企业单位在人事制度改革中对员工进行分流，被分流的入员当年可在原单位领取原工资的100%，从第二年起每年只在原单位领取前一年工资的
正确答案
3
解析
解析已在路上飞奔，马上就到！
知识点
9.已知公比不为1的等比数列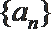
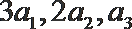
A
B
C121
D31
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．已知各项均为正数的等比数列
A
B
C
D不存在
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．已知等比数列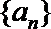
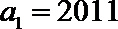
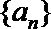
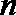
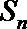
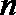
（1）证明：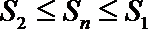
（2）判断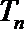
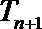
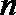
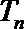
（3）证明：若数列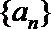
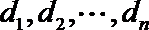
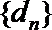
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15． 已知公差不为0的等差数列
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
21．已知椭圆
（1）求椭圆的方程；
（2）设不过原点
正确答案
（1）
（2）
解析
解析已在路上飞奔，马上就到！
知识点
6．各项均为正数的等比数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
19．某校为扩大教学规模，从今年起扩大招生，现有学生人数为b人，以后学生人数年增长率为4.9‰．该校今年年初有旧实验设备a套，其中需要换掉的旧设备占了一半。学校决定每年以当年年初设备数量的10%的增长率增加新设备，同时每年换掉x套的旧设备。
（1）如果10年后该校学生的人均占有设备的比率正好比目前翻一番，那么每年应更换的旧设备是多少套？
（2）依照（1）的更换速度，共需多少年能更换所有需要更换的旧设备？
下列数据供计算时参考：
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．下列命题中，真命题是__________（写出所有真命题的序号）
①
②
③
④
正确答案
③④
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析