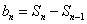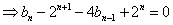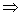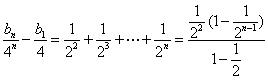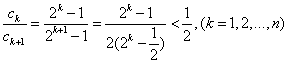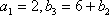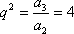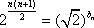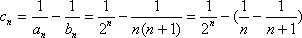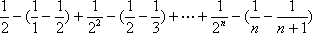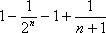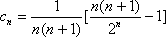- 等比数列的性质及应用
- 共180题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知等比数列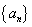
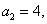
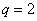
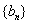
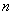
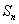
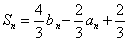

(1)求数列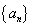
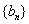
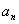
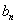
(2)设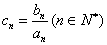
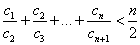
正确答案
见解析。
解析
(1) 解法一:由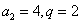
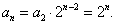
由上式结合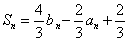
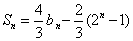
则当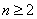
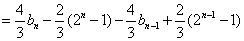
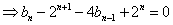
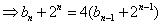
∵
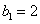
∴数列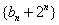
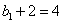
∴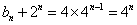
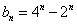
【解法二:由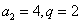
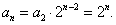
由上式结合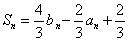
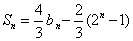
则当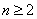
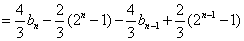
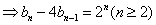
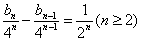
∴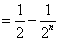
∵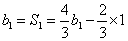
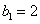
∴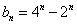
(2) 由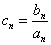
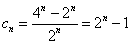
【或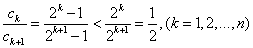
∴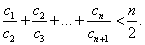
知识点
已知数列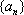
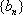
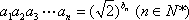
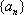
(1) 求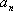
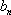
(2) 设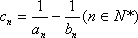


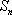
(i)求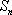
(ii)求正整数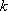
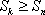
正确答案
见解析
解析
(1)∵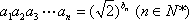
当n≥2,n∈N*时,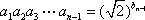
由①②知:当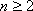
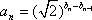
∵b3=6+b2, ∴a3=8。
∵{an}为等比数列,且a1=2,∴{an}的公比为q,则
由题意知an>0,∴q>0,∴q=2。
∴an=2n(n∈N*)。
又由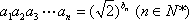
即
∴bn=n(n+1)(n∈N*)。
(2)(i)∵
∴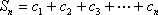
=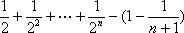
=
(ii)因为c1=0,c2>0,c3>0,c4>0;
当n≥5时,
而
所以,当n≥5时,cn<0,
综上,对任意n∈N*恒有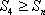
知识点
等比数列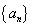
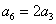
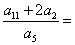
正确答案
5
解析
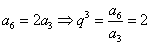
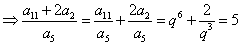
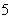
知识点
数列

正确答案
解析
略
知识点
已知数列




(1)对任意实数

(2)试判断数列
正确答案
见解析
解析
(1)证明:假设存在一个实数


即
所以
(2)因为
又
所以当



当




故当



知识点
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
(1)证明:BC1∥平面A1CD;
(2)求二面角D-A1C-E的正弦值。
正确答案
见解析
解析
(1)连结AC1交A1C于点F,则F为AC1中点。
又D是AB中点,连结DF,则BC1∥DF.
因为DF⊂平面A1CD,BC1
所以BC1∥平面A1CD.
(2)
由AC=CB=
以C为坐标原点,
设CA=2,则D(1,1,0),E(0,2,1),A1(2,0,2),


设n=(x1,y1,z1)是平面A1CD的法向量,
则
可取n=(1,-1,-1)。
同理,设m是平面A1CE的法向量,
则
从而cos〈n,m〉=
故sin〈n,m〉=
即二面角D-A1C-E的正弦值为
知识点
从1,2,3,





正确答案
解析
略
知识点
若数列{an}的前n项和为Sn,则下列命题正确的是( )
正确答案
解析
解:A:数列{an}的前n项和为Sn,故 Sn =a1+a2+a3+…+an,
若数列{an}是递增数列,则数列{Sn}不一定是递增数列,如an=n﹣60,当an<0 时,数列{Sn}是递减数列,故A不正确。
B:由数列{Sn}是递增数列,不能推出数列{an}的各项均为正数,
如数列:0,1,2,3,…,满足{Sn}是递增数列,但不满足数列{an}的各项均为正数,故B不正确。
C:若{an}是等差数列(公差d≠0),则由S1•S2…Sk=0不能推出a1•a2…ak=0,
例如数列:﹣3,﹣1,1,3,满足S4=0,但 a1•a2•a3•a4≠0,故C不正确。
D:一方面:若{an}是等比数列,则由S1•S2…Sk=0(k≥2,k∈N),
从而当k=2时,有S1•S2=0⇒S2=0⇒a1+a2=0,
∴a2=﹣a1,从而数列的{an}公比为﹣1,故有ak+ak+1=ak﹣ak=0。
另一方面,由ak+ak+1=0可得ak=﹣ak+1,∴a2=﹣a1,
可得S2=0,∴S1•S2…Sk=0(k≥2,k∈N),故D正确。
故选D。
知识点
扫码查看完整答案与解析