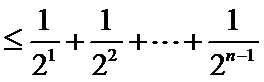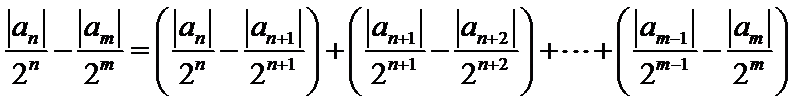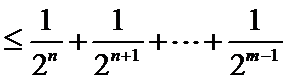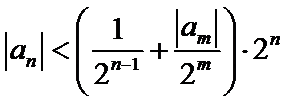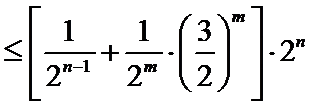- 等比数列的性质及应用
- 共180题
13.设数列




正确答案
1;121
知识点
8.已知{an}是等差数列,Sn是其前n项和.若a1+a22=
正确答案
20
知识点
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
若无穷数列




(1) 若







(2) 若无穷数列






(3) 设





正确答案
(1)
∴
∴
∴
∴
∴
(2)设



∴
∴
∴
∴
∴
∵
而

故
(3) 充分性:若
则
若存在

则
故
必要性:若对任意

则
设函数
由

∴一定能找到一个
∴
∴
故
∴
知识点
17.已知数列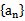
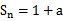
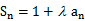
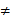
(I)证明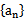
(II)若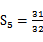
正确答案
见解析
解析
(Ⅰ)由题意得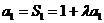
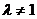
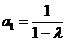
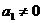
由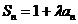
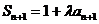
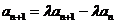
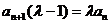
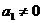
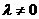
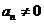
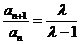
因此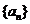
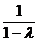
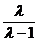
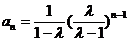
(Ⅱ)由(Ⅰ)得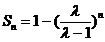
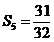
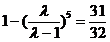
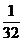
解得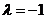
知识点
设数列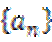
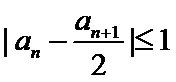
24.求证:
25.若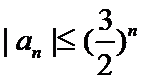
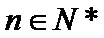
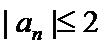
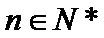
正确答案
由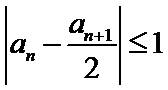
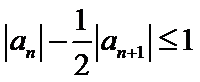
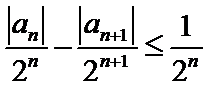
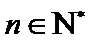
所以
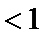
因此
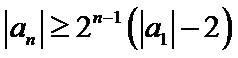
解析
见答案
考查方向
解题思路
先利用三角形不等式得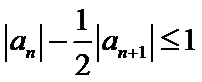
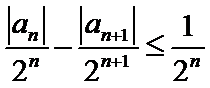
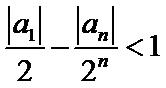
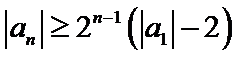
正确答案
任取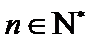
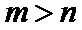
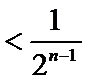
故
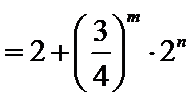
从而对于任意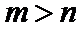
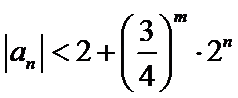
由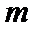
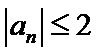
否则,存在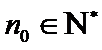
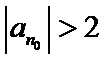
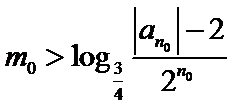
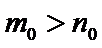
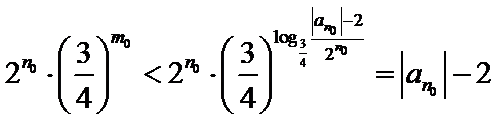
与①式矛盾.
综上,对于任意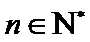
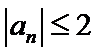
解析
见答案
考查方向
解题思路
由(I)可得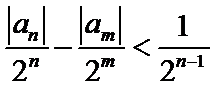
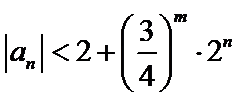
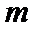
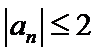
15.设等比数列
正确答案
解析
试题分析:设等比数列的公比为








考查方向
解题思路
先根据等比数列的通项公式求出通项,进而即可求出a1a2 …an的最大值。
易错点
不能准确记忆等比数列的通项公式、性质导致出错。
知识点
17.已知无穷等比数列




正确答案
考查方向
知识点
已知数列
21.求数列
22.设




正确答案
(Ⅰ)
解析
(Ⅰ)由题设可知
又


由


考查方向
解题思路
先根据特殊项的值和关系,然后解出首项和公比
易错点
求数列通项公式时,不会利用数列的性质简便求解
正确答案
(Ⅱ)
解析
(Ⅱ)
又
所以

考查方向
解题思路
根据前n项和公式,整理得到裂项相消法得到新数列的和
易错点
求和时的方法选错或不会用裂项相消法求和
4.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()
正确答案
解析
由题意,要组成没有重复的五位奇数,个位数为1、3、5中的一个,其它位置随意排列有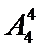
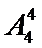
考查方向
解题思路
利用排列组合计数时,关键是正确进行分类和分步,分类时要注意不重不漏,分步时要注意整个事件的完成步骤.在本题中,个位是特殊位置,第一步应先安排这个位置,第二步再安排其他四个位置
易错点
本题考查排列组合问题,容易在分类和分布中发生问题
知识点
11.观察下列各式:
……
照此规律,当n

正确答案
4n﹣1
解析
因为
…
照此规律,可以看出等式左侧最后一项,组合数的上标与等式右侧的幂指数相同,
可得:当n∈N*时,
故答案为:4n﹣1.
考查方向
解题思路
仔细观察已知条件,找出规律,即可得到结果.
易错点
归纳推理;组合及组合数公式.菁优网版权所有
知识点
扫码查看完整答案与解析