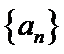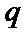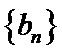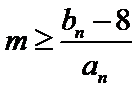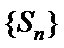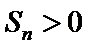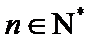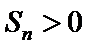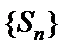- 等比数列的性质及应用
- 共180题
10. 已知单调递减的等比数列
则公比
正确答案
解析
因为
考查方向
解题思路
根据等比数列的特点，利用方程的思想解出
易错点
忽略题中的单调递减条件
知识点
3.已知
比数列，则（ ）
A
B
C
D
正确答案
解析
试题分析：利用公差不为0的等差数列中
设等差数列{
故选B.
考查方向
解题思路
根据等差数列的通项公式，等比数列的性质，求出首项和公差d的关系，然后利用首项表示出前4项和，判断出符号．
易错点
要熟记的等差数列和等比数列的通项公式和前n项和公式.
知识点
2．设{an}是公比为q的等比数列，则“q>1”是“{an}为递增数列”的( )
正确答案
解析
根据指数函数的单调性，举反例：首项
考查方向
本题考查等比数列的单调性，充分条件与必要条件.
解题思路
等比数列的增减是由首项与公比确定的，当首项
易错点
对递增等比数列判断不准，对条件的性质判断不准.
知识点
18. 已知等比数列
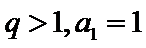
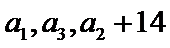
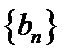
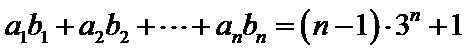
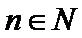
（I）求数列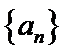
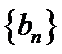
（II）若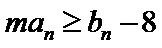
正确答案
见解析
解析
考查方向
解题思路
1）借助等差数列性质求出
2）利用由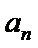
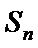
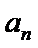
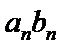
3）对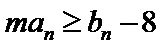
4）讨论新数列单调性，并求出最值
易错点
本题第一问忽略验证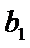
知识点
已知等比数列
22.求数列
23.求数列
正确答案
（1）
解析
（1）设
故方程有两个不同的实根，由
从而
考查方向
解题思路
1）第一问设
2）第二问
易错点
错位相减法求和计算容易错。
正确答案
（2）
解析
（2）由（1）知
考查方向
解题思路
1）第一问设
2）第二问
易错点
错位相减法求和计算容易错。
3.在等比数列
A
B
C
D
正确答案
解析
由
考查方向
解题思路
先利用等比数列的性质求出
易错点
易直接利用基本量得到关于首相和公比的方程组解方程出错，误选B。
知识点
6. 设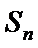
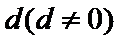
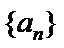
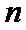
A若
B若数列
C若数列
D若对任意
正确答案
解析
通过对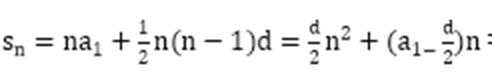
考查方向
解题思路
根据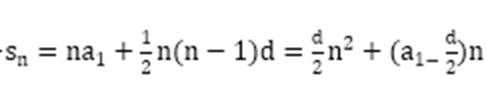
易错点
对等差数列的前n项和公式的函数性质没有掌握
知识点
已知
22.求数列
23.设
正确答案
（1）
解析
（1）因为
所以
所以
考查方向
解题思路
1.第（1）问根据等差数列、等比数列的基本量求出通项公式；2.根据第（1）问求出
易错点
1.不会将
正确答案
（1）
解析
（2）
所以
(或
因为
所以，不存在正整数
考查方向
解题思路
1.第（1）问根据等差数列、等比数列的基本量求出通项公式；2.根据第（1）问求出
易错点
1.不会将
16. 已知等比数列{an}中a2=1，则其前3项的和S3的取值范围是 。
正确答案
解析
设首项为a（显然a不为0）. 公比为q（显然q不为0）
当q=1时
考查方向
解题思路
对公比q分类讨论，再结合a2=1，将S3转成关于q函数进行讨论。
易错点
对公式q的讨论及范围的确定
知识点
11.设等比数列
正确答案
32（
解析
根据题意依次算出等比数列的前四项，分别为
考查方向
解题思路
根据题意依次算出等比数列的前四项，分别为16，16，44，54，可判断出第二项不可能是16，所以该组数据中出错的是
易错点
本题易在“检验后发现其中恰好一个数算错了” 这句话理解上出错.
知识点
扫码查看完整答案与解析