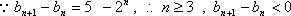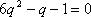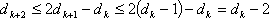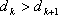- 等比数列的性质及应用
- 共180题
如果无穷数列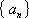
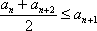
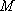

其中

(1)设数列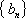
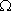
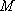
(2)设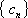
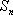
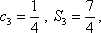
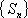
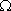
(3)设数列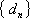

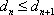
正确答案
见解析
解析
(1)
故,数列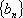
当
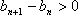
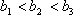
则数列
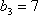
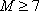
(2) 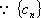
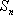
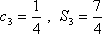
设其公比为
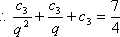
整理,得
解得 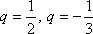

对任意的
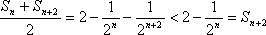
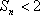
故
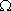
(3)假设存在正整数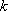
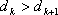

可得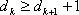
即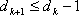

所以,
由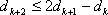
得 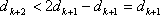

因为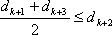
所以
由此类推,可得
又存在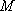
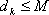
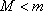
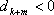
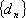

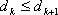
知识点
已知数列


(1)若

(2)记


(3)若

正确答案
见解析
解析
(1)



又
求交集得:




(2)由
故


(3)由(1)有


由(2)可知


故

所以


因此
即


知识点
已知无穷数列{an}中,a1,a2,a3,…,am是首项为10.公差为-2的等差数列;am+1,am+2,…,a2m是首项为

n∈N*,均有an+2m=an成立。
(1)当m=12时,求a2012;
(2)若
(3)若数列{an}的前n项和为sn,试判断是否存在m(m≥3,m∈N*),使得S128m+4≥
2012成立?若存在,试求出m的值;若不存在,请说明理由。
正确答案
见解析。
解析
(1)m=12时,数列的周期为24.
∵2012=24×83+20,而a20是等比数列中的项。

(2)设am+k是第一个周期中等比数列中的第k项,则
∴等比数列中至少有7项,即m≥7.则一个周期中至少有14项。
∴a52最多是第三个周期中的项。
着a52是第一个周期中的项,则
∴m=52-7=45
若a52是第二个周期中的项,则
∴3m=45,m=15;
若a52是第三个周期中的项,则
∴5m=45,m=9;
综上,m=45.或15.或9。
(3)2m是此数列的周期,
又∵等差数列的前4项的和为;10+8+6+4=28
∴S2m是最大时,S128m+4最大。

当m≤5时,S2m是关干m的递增函数且
当m≥7时,
∴当m=6时,S2m取得最大值,则S128m+4取得最大值为
由此可知,不存在m(m≥3。m∈N*),使得S128m+4≥2012成立,
知识点
设




正确答案
解析
由

知识点
已知函数

(1)当α=1时,求数列{an}的通项公式;
(2)在(1)的条件下,证明对∀n∈N*有:
(3)若α=2,且对∀n∈N*,有0<an<1,证明:
正确答案
见解析。
解析
(1)当α=1时,

故数列



(2)证法1:由(1)知

∴a1a2a3+a2a3a4+…+anan+1an+2=
=

[证法2:①当n=1时,等式左边=
等式右边=
②假设当n=k(k≥1)时等式成立,
即
则当n=k+1时
=
=
这就是说当n=k+1时,等式成立,
综①②知对于∀n∈N*有:
(3)当α=2时,

∵0<an<1,
∴



∵an=1﹣an与
即对∀n∈N*,

则
又0<an<1,∴
∴an+1>an,∴an∈[
令

当


知识点
扫码查看完整答案与解析