- 等比数列的性质及应用
- 共180题
若集合



①当

②当

③当

……
由以上结论,推测出一般结论:
当
正确答案
解析
因为当有两个集合时,




知识点
已知{an} 为等比数列,a4+a7=2,a5a6=﹣8,则a1+a10=( )
正确答案
解析
∵ a4+a7=2,由等比数列的性质可得,a5a6=a4a7=﹣8
∴ a4=4,a7=﹣2或a4=﹣2,a7=4
当a4=4,a7=﹣2时,
∴ a1=﹣8,a10=1,
∴ a1+a10=﹣7
当a4=﹣2,a7=4时,q3=﹣2,则a10=﹣8,a1=1
∴ a1+a10=﹣7
综上可得,a1+a10=﹣7
故选D
知识点
己知各项均不相等的等差数列{an}的前四项和S4=14,且a1,a3,a7成等比数列。
(1)求数列{an}的通项公式;
(2)设Tn为数列
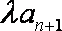
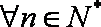
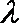
正确答案
见解析
解析
(1)设公差为d.由已知得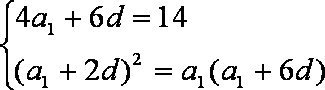
解得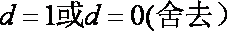
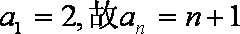
(2)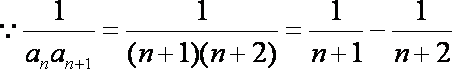
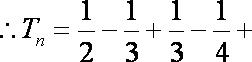
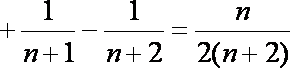
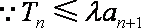
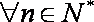
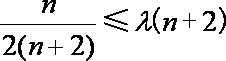
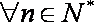
又
∴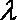

知识点
等比数列{
正确答案
2
解析
由已知得:
两边约掉

解得:



故答案为:2
知识点
已知数列








(1)若

(2)是否存在正整数k,使

正确答案
见解析
解析
解析:(1)由题意知,

∴


∴





∴


(2)记




① 若



② 若



③ 若



因为

综上:不存在
知识点
扫码查看完整答案与解析






