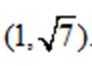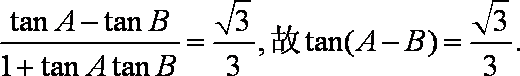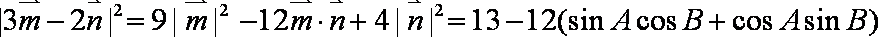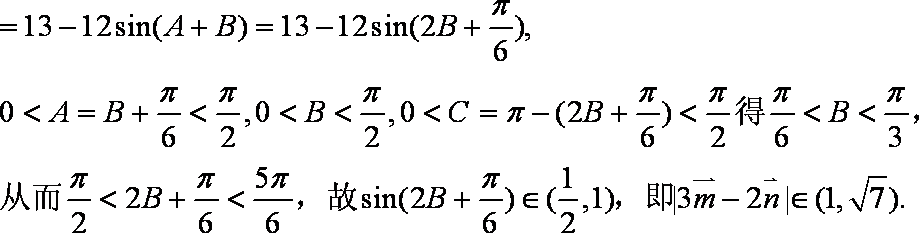- 等比数列的性质及应用
- 共180题
已知正项数列满足
(1)求数列
(2)设

正确答案
见解析
解析
(1)整理得
又

(2)由(1)知
所以
知识点
在锐角三角形ABC中,已知角A、B、C所对的边分别为a、b、c,且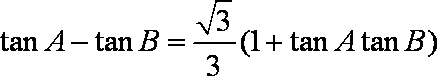
(1)若c2=a2+b2—ab,求角A、B、C的大小;
(2)已知向量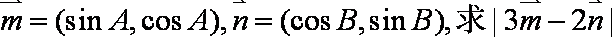
正确答案
(1)A= 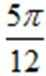
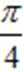
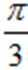
解析
(1)由已知得
(2)
知识点
已知函数


(1)证明sinθ=1,并求f(x)的解析式。
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式
(3)已知数列



正确答案
见解析
解析
解析:(1)∵
由题设可知:

从而a=


∴f(x)=
(2)
(i)当m>1时,f(x)在[m,m+3]上递增。故f(x)max=f(m+3),f(x)min=f(m)
由f(m+3)-f(m)=



(ii)当0≤m≤1时,f(x)在[m,1]上递减,在[1,m+3]上递增。
∴f(x)min=f(1),f(x)max={f(m),f(m+3)}max
又f(m+3)-f(m)=3m2+12m+

∴|f(x1)-f(x2)| ≤f(x)max-f(x)min=f(m+3)-f(1) ≤f(4)-f(1)=
故当0≤m≤1原式恒成立。 (8分)
综上:存在m且m∈[0,1]合乎题意。 (9分)
(3)∵ a1∈ (0,1

假设n=k(k≥2,k∈N*)时,ak>2。则ak+1=f(ak)>f(2)=8>2
故对于一切n(n≥2,n∈N*)均有an>2成立。 (11分)
令g(x)=
得
当x∈(0,2)时

∴g(x)在x∈[2,+∞
而g(2)=8-8ln2>0,即当x∈[2,+∞
∴g(an)>0,(n≥2)也恒成立。即:an+1>8lnan(n≥2)恒成立。
而当n=1时,a2=8,而8lna1≤0,∴a2>8lna1显然成立。
综上:对一切n∈N*均有an+1>8lnan成立。 (13分)
知识点
已知




(1) 求

(2) 设

正确答案
(1)


解析
(1)设




设



所以
(2)

②-①得:
所以
知识点
设同时满足条件:①












(1)求
(2)设



正确答案
见解析
解析
(1)因为
当




∴
(2)由(1)知,
若
则有


故

再将


由于①
(或做差更简单:因为

②

所以符合①②,故
知识点
扫码查看完整答案与解析