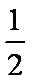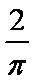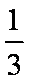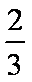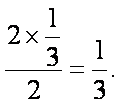- 概率与统计
- 共1335题
甲、乙两人玩掷骰子游戏:甲先掷一个骰子,记下向上的点数;然后乙再掷,同样记下向上的点数.如果两人所掷点数之和为偶数则甲胜,否则乙获胜。
(1)求甲胜且点数之和为6的事件发生的概率;
(2)这种游戏规则公平吗?用你所学的知识说明理由。
正确答案
见解析。
解析
(1)设“甲胜且点数的和为6”为事件

则
两人掷骰子的结果包括(1,1),(1,2),…,(1,5),(1,6),(2,1),…,(6,1),…,(6,6)共36个基本事件;
事件
所以
所以,甲胜且点数之和为6的概率为
(2)这种游戏公平。
设“甲胜”为事件B,“乙胜”为事件C.甲胜即两个点数的和为偶数.
所包含基本事件为以下18个:(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3)(5,5),(6,2),(6,4),(6,6)
所以甲胜的概率为
乙胜的概率为
所以这种游戏是公平的
知识点
甲、乙两校各有3名教师报名支教,期中甲校2男1女,乙校1男2女。
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
正确答案
见解析。
解析
甲校的男教师用A、B表示,女教师用C表示,乙校的男教师用D表示,女教师用E、F表示,
(1)根据题意,从甲校和乙校报名的教师中各任选1名,
有(AD),(AE),(AF),(BD),(BE),(BF),(CD),(CE),(CF),共9种;
其中性别相同的有(AD)(BD)(CE)(CF)四种;
则选出的2名教师性别相同的概率为P=
(2)若从报名的6名教师中任选2名,
有(AB)(AC)(AD)(AE)(AF)(BC)(BD)(BE)(BF)(CD)(CE)(CF)(DE)(DF)(EF)共15种;
其中选出的教师来自同一个学校的有6种;
则选出的2名教师来自同一学校的概率为P=
知识点
某小组共有么、B、C、D、E五位同学,他们高三一模的数学成绩以及语文成绩如下表所示:
(1)从该小组数学成绩低于l20分的同学中任选2人,求选到的2人数学成绩都在110分以下的概率;
(2)从该小组同学中任选2人,求选到的2人的数学成绩都在90以上且语文成绩都在[86,110)中的概率。
正确答案
见解析
解析
(1)从数学分数低于120的同学中任选2人,其一切可能的结果组成的基本事件有:

由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的。
选到的2人的数学成绩都在110分以下的事件有:
因此选到的2人数学成绩都在110以下的概率为P=

(2)从该小组同学中任选2人,其一切可能的结果组成的基本事件有:
由于每个人被选到的机会均等,因此这些基本事件的出现是等可能的。
选到的2人的数学成绩都在90以上且语文成绩都在[86,110)中的事件有:
因此选到的2人的数学成绩都在90以上且语文成绩都在[86,110)中的概率为P=
知识点
i是虚数单位,复数
正确答案
解析
由

所以其共轭复数为3﹣4i。
知识点
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组


(1)若成绩大于或等于14秒且小于16秒
认为良好,求该班在这次百米测试中
成绩良好的人数;
(2)设

测试成绩,且已知
求事件“
正确答案
见解析
解析
解:(1)由直方图知,成绩在

所以该班成绩良好的人数为27人.
(2)由直方图知,成绩在




成绩在





若



若


共有12种情况.
所以基本事件总数为21种
事件“
∴P(

知识点
在区间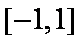
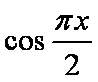
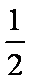
正确答案
解析
试题分析:本题是求几何概型概率,测度为长度.由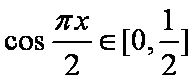
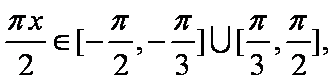
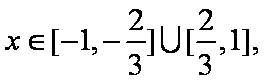
知识点
现有编号分别为1,2,3,4,5的五个不同的语文题和编号分别为6,7,8,9,的四个不同的数学题。甲同学从这九个题中一次随机抽取两道题,每题被抽到的概率是相等的,用符号(x,y)表示事件“抽到的两题的编号分别为x、y,且
(1)共有多少个基本事件?并列举出来;
(2)求甲同学所抽取的两题的编号之和小于17但不小于11的概率。
正确答案
见解析
解析
解:(1)共有




































(2)















知识点
某初中校共有学生1200名,各年级男、女生人数如下表:
已知在全校学生中随机抽取l名,抽到七年级女生的概率是0.17。
(1)求a的值;
(2)现用分层抽样的方法在全校抽取200名学生,问应在九年级抽取多少名学生?
(3)已知175≤b≤183,求九年级中女生不少于男生的概率。
正确答案
见解析。
解析
(1)由题意,得a=1200×0.17=204;
(2)由(1)及已知条件,得
七年级共有学生:204+198=402(名)。
八年级共有学生:216+222=438(名)。
所以九年级共有学生:1200﹣402﹣438=360(名)。
所以应在九年级抽取学生数:360×
(3)由(2)可知九年级共有学生360名。
则九年级中女生人数及男生人数的所有可能结果为:
(175,185),(176,184),(177,183),(178,182),(179,181),(180,180),(181,179),(182,178),(183,177)共9中。
其中女生不少于男生的可能结果为:(180,180),(181,179),(182,178),(183,177)共4种。
所以九年级中女生不少于男生的概率为:P=
知识点
爸爸和亮亮用4张扑克牌(方块2,黑桃4,黑桃5,梅花5)玩游戏,他俩将扑克牌洗匀后,背面朝上放置在桌面上,爸爸先抽,亮亮后抽,抽出的牌不放回。
(1)若爸爸恰好抽到了黑桃4。
①请把右面这种情况的树形图绘制完整;
②求亮亮抽出的牌的牌面数字比4大的概率。
(2)爸爸、亮亮约定,若爸爸抽到的牌的牌面数字比亮亮的大,则爸爸胜;反之,则亮亮赢,你认为这个游戏是否公平?如果公平,请说明理由,如果不公平,更换一张扑克牌使游戏公平。
正确答案
(1) 
解析
(1)由于抽出的牌不放回,亮亮抽出的牌只能为方块2,黑桃5,梅花5这三种,因此树形图对应三种情况. 亮亮抽出的牌的牌面数字比4大的事件数就是统计结果中纵坐标数字大于4的结果数为2,因此所求概率为
列出所有情况的树形图:

统计出爸爸抽到的牌的牌面数字比亮亮的大,即有5种情况,因此爸爸胜的概率只有

试题解析:(1) ① 树形图:
②所以亮亮抽出的牌的牌面数字比4大的概率是
(2)不公平,理由如下:
爸爸抽出的牌的牌面数字比亮亮的大有5种情况,其余均为小于等于亮亮的牌面数字
所以爸爸胜的概率只有
只需把黑5改成3即可
知识点
为了了解低保户的生活情况,用分层抽样的方法从
(1)求
(2)若从

正确答案
见解析
解析
(1)分层抽样的抽样比为
∴ 

(2)记从





选中的2个低保户都来自

∴ 选中的2户都来自

知识点
某学校高三(1)班学生举行新年联欢活动,准备了5张标有1,2,3,4,5的外表完全相同的卡片,规定通过游戏来决定抽奖机会,每个获得抽奖机会的同学,一次从中任意抽取2张卡片,两个卡片中的数字之和为5时获一等奖,两个卡片中的数字之和能被3整除时获二等奖,其余情况均没有奖。
(1)共有几个一等奖?几个二等奖?
(2)求从中任意抽取2张,获得一等奖的概率;
(3)一名同学获得两次抽奖机会,求①获得一个一等奖和一个二等奖的概率:②两次中至少一次获奖的概率。
正确答案
见解析。
解析
(1)从5张卡片中任取两张,共有
(2,4),(2,5),(3,4),(3,5),(4,5),一等奖2个为(1,4),(2,3),二等奖4个为(1,2),
(1,5),(2,4),(4,5)。
(2)从中任意抽取2张,获得一等奖的概率P=
(3)一名同学获得两次抽奖机会,
①获得一个一等奖和一个二等奖的概率
②两次均没获奖的概率
两次中至少一次获奖的概率为
知识点
已知椭圆:

(1)求椭圆的方程。
(2)Q是椭圆上位于x轴下方的一点,F1F2分别是椭圆的左、右焦点,直线QF1的倾斜角为
(3)以B为直角顶点作椭圆的内接等腰直角三角形ABC,判断这样的三角形存在吗?若存在,有几个?若不存在,请说明理由。
正确答案
见解析。
解析
(1)依题意,b=1,因为离心率等于
所以
所以椭圆方程为:
(2)F1(﹣


得


所以


(3)假设这样的三角形存在,设AB的方程为y=kx+1(k>0),则BC的方程为y=﹣
由

由

因为|AB|=|BC|,得:
将yA=kxA+1,


将①②代入得:k2(4+k2)2=(4k2+1)2,即[k(4+k2)+1+4k2][k(4+k2)﹣(1+4k2)]=0,
因为k>0,k(4+k2)+1+4k2>0,得(k﹣1)(k2﹣3k+1)=0,
解得k=1,k=

所以存在这样的等腰直角三角形。
知识点
某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分。已知甲、乙两位选手抢到答题权的概率均相同,且每道题是否答对的机
(1)求甲抢到1题的概率;
(2)求甲得到10分的概率。
正确答案
见解析
解析
(1)P=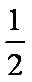
(2)甲得分的情况一共有16种情况,若两道题都是甲答,则甲得分情况为:(0,0),(20,0),(0,20),(20,20),
若甲答第一题,乙答第二题,则甲得分情况为:(20,0)(20,10)(0,0)(0,10)。
若乙答第一题,甲答第二题,则甲得分情况为:(0,20)(0,0)(10,20)(10,0)。10分若两题都是乙答,则甲得分情况为:(0,0),(0,10),(10,0),(10,10)。所以甲得10分的概率为:
知识点
城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客需求,为此,渭南市公交公司在某站台的60名候车乘客中随机抽取15人, 将他们的候车时间作为样本分成5组,如下表所示(单位:min):
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中选2人作进一步的问卷调查,求抽到的两人恰好来自同一组的概率。
正确答案
见解析。
解析
(1)候车时间少于10分钟的概率为
所以候车时间少于10分钟的人数为
(2)将第三组乘客编号为






其中两人恰好来自不同组包含7个基本事件,所以,所求概率为
知识点
某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续驶里程数R(单位:公里)分为3类,即A:80≤R<150,B:150≤R<250,C:R≥250,对这140辆车的行驶总里程进行统计,结果如下表:
(1)从这140辆汽车中任取1辆,求该车行驶总里程超过5万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从C类车中抽取了n辆车。
(ⅰ)求n的值;
(ⅱ)如果从这n辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率。
正确答案
(1)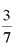
解析
(1)从这140辆汽车中任取1辆,则该车行驶总里程超过5万公里的概率为
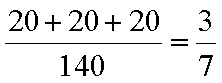
(2) (ⅰ)依题意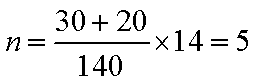
(ⅱ)5辆车中已行驶总里程不超过5万公里的车有3辆,记为A,B,C;
5辆车中已行驶总里程超过5万公里的车有2辆,记为M,N。
“从5辆车中随机选取2辆车”的所有选法共10种: AB,AC ,AM,AN,BC,BM,BN,CM,CN,MN。
“从5辆车中随机选取2辆车,恰有一辆车行驶里程超过5万公里”的选法共6种: AM,AN,BM,BN,CM,CN。
设“选取2辆车中恰有一辆车行驶里程超过5万公里”为事件D,
则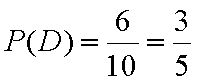
选取2辆车中恰有一辆车行驶里程超过5万公里的概率为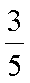
知识点
扫码查看完整答案与解析