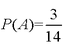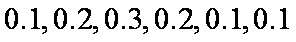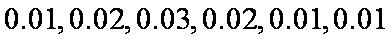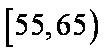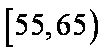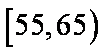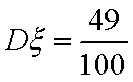- 概率与统计
- 共1335题
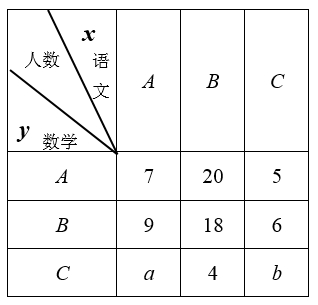
已知高二某班学生语文与数学的学业水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示语文成绩与数学成绩,例如:表中语文成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18。
(1)求抽取的学生人数;
(2)设该样本中,语文成绩优秀率是30%,求a,b值;
(3)已知
正确答案
(1)100(2)17(3)
解析
解析:
(1)由题意可知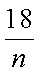
(2)由(1)知n=100,所以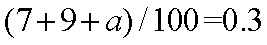
而7+9+a+20+18+4+5+6+b=100,故b=17. ………………6分
(3)设“语文成绩为A等级的总人数比语文成绩为C等级的总人数少”为事件A,
由(2)易知a+b=31,且a≥10,b≥8, ………………7分
满足条件的(a,b)有
(10,21),(11,20),(12,19),(13,18), (14,17),
(15,16),(16,15
(20,11),(21,10),(22,9),(23,8),共有14组, ………………10分
其中b+11
则所求概率为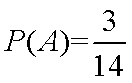

知识点

(1)写出频率分布直方图中的
(2)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为



(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量.
正确答案
见解析
解析
(1)

(2)
(3)乙种酸奶平均日销售量为:

乙种酸奶未来一个月的销售总量为:
知识点
在平面直角坐标系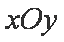
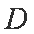

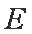
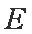

正确答案
解析
略
知识点
有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”.四位歌手的话只有两句是对的,则获奖的歌手是 。
正确答案
答案:丙
解析
略
知识点
为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
附:
参照附表,得到的正确结论是
正确答案
解析
略
知识点
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率。
正确答案
见解析
解析
解:(1)设“从该批电器中任选1件,其为”B”型”为事件A1,
则
所以从该批电器中任选1件,求其为”B”型的概率为
(2)设“从重量在[80,85)的5件电器中,任选2件电器,求其中恰有1件为”A”型”为事件A2,记这5件电器分别为a,b,c,d,e,其中”A”型为a,b,从中任选2件,所有可能的情况为ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种
其中恰有1件为”A”型的情况有ac,ad,ae,bc,bd,be,共6种
所以

知识点
某学校为了增强学生对数学史的了解,提高学生学习数学的积极性,举行了一次数 学史知识竞赛,其中一道题是连线题,要求将4名数学家与他们所著的4本著作一 对一连线,规定:每连对一条得5分,连错一条得-2分.某参赛者随机用4条线把 数学家与著作一对一全部连接起来
(1)求该参赛者恰好连对一条的概率。
(2)求该参赛者得分不低于6分的概率。
正确答案
(1)
解析
记4名数学家分别为

(4分)
其中恰好连对一条的情形有如下8种:
恰好连对两条的情形有如下6种:
全部连对的情形只有1种:

(1) 恰好连对1条的概率为
(2) 得分不低于6分即全部连对或恰好连对2条的概率为
知识点
某高中共有
的方法从中抽取
正确答案
16
解析
略
知识点
已知函数
(1)从区间





(2)若连续掷两次骰子(骰子六个面上标注的点数分别为






正确答案
见解析
解析
解:(1)







(2)由已知:






当





当



而基本事件总数为

知识点
某在元宵节活动上,组织了“摸灯笼猜灯谜”的趣味游戏.已知在一个不透明的箱子内放有大小和形状相同的标号分别为1,2,3的小灯笼若干个,每个灯笼上都有一个谜语,其中标号为1的小灯笼1个,标号为2的小灯笼2个,标号为3的小灯笼n个.若参赛者从箱子中随机摸取1个小灯笼进行谜语破解,取到标号为3的小灯笼的概率为
(1)求n的值;
(2)从箱子中不放回地摸取2个小灯笼,记第一次摸取的小灯笼的标号为a,第二次摸取的小灯笼的标号为b.记“
正确答案
见解析
解析
(1)由题意,
(2)记标号为2的小灯笼为

(1, 





















知识点
2013年12月21日上午10时,省会首次启动重污染天气Ⅱ级应急响应,正式实施机动车车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
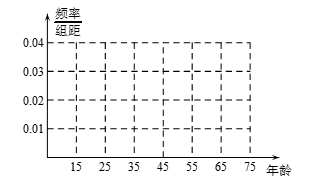
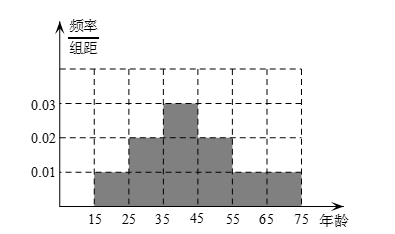
(1)完成被调查人员的频率分布直方图;
(2)若从年龄在[55,65),[65,75)的被调查者中各随机选取1人进行进行追踪调查,求两人中至少有一人赞成“车辆限行”的概率。
正确答案
见解析
解析
(1)各组的频率分别是
所以图中各组的纵坐标分别是
……………………5分
(2)设A表示事件:年龄在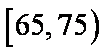
则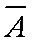
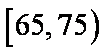
从年龄在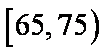
…………………7分
记年龄在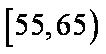
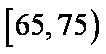
两人都不赞成“车辆限行”的所有可能结果为:ac,bc. ………………10分
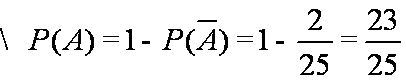
知识点
右图是依据某城市年龄在20岁到45岁的居民上网情 况调查而绘制的频率分布直方图,现已知年龄在 [30,35)、[35,40)、[40,45]的上网人数呈现递减的等差数列分布,则年龄在[35,40)的网民出现的频率为
正确答案
解析
由









知识点
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重。大气污染可引起心悸、呼吸困难等心肺疾病。为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
已知在全部50人中随机抽取1人,抽到患心肺疾病的人的概率为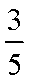
(1)请将上面的列联表补充完整;
(2)是否有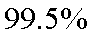
(3)已知在患心肺疾病的10位女性中,有3位又患胃病,现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为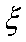
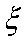
下面的临界值表供参考:
(参考公式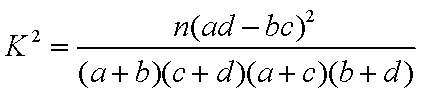
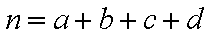
正确答案
见解析。
解析
(1):列联表补充如下 ………2分
(2):因为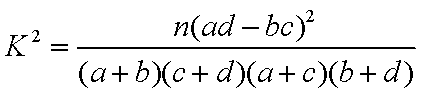
又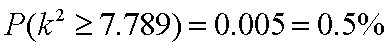
那么,我们有
(3): 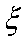
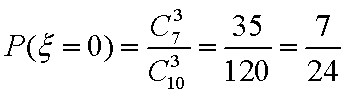
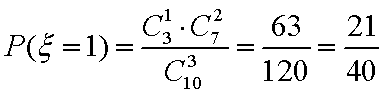
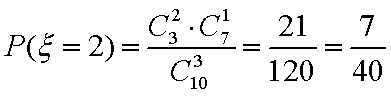
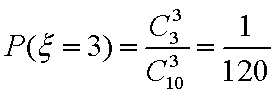
分布列如下: ………8分
则
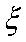
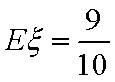
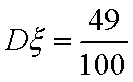
知识点
某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样的方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
正确答案
(1)有关(2)3名(3)
解析
(1)有关,收看新闻节目的观众多为年龄大的. ………………………………………3分
(2)应抽取的人数为:
(3)由(2)知,抽取的5名观众中,有2名观众的年龄处于20至40岁,
3名观众的年龄大于40岁. ………………………………………………………………8分
所求概率为:
知识点
某电视台举办青年歌手大奖赛,有10名评委打分,已知甲、乙两名选手演唱后的打分情况如茎叶图所示:
(1)从统计的角度,你认为甲与乙比较,演唱水平怎样?
(2)现场有3名点评嘉宾A、B、C,每位选手可以从中选2位进行指导,若选手选每位点评嘉宾的可能性相等,求甲乙两选手选择的点评嘉宾恰重复一人的概率。
正确答案
见解析。
解析
(1)由茎叶图可得:


所以甲演唱水平更高一点,但甲的方差较大,即评委对甲的水平认可存在较大的差异
(2)依题意,共有9个基本事件:
其中,甲乙两选手选择的点评嘉宾恰重复一人包含6个基本事件。
所以,所求概率为
知识点
扫码查看完整答案与解析