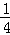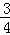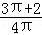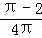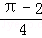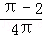- 概率与统计
- 共1335题
某数学兴趣小组有男女生各


(1)求

(2)现从成绩高于
取的两名同学恰好为一男一女的概率.
正确答案
见解析。
解析
(1) 男生成绩为



其中位数为

女生成绩为



平均数为
解之得
(2) 设成绩高于



设成绩高于





从高于









其中恰好为一男一女的取法:







因为
故抽取的两名同学恰好为一男一女的概率为
知识点
以下茎叶图记录了甲组3名同学寒假假期中去图书馆A学习的次数和乙组4名同学寒假假期中去图书馆B学习的次魏乙组记录中有一个数据模糊,无法确认,在圈中以x表示。
(1)如果x=7,求乙组同学去图书馆学习次数的平均数和方差;
(2)如果x=9,从学习次数大于8的学生中选两名同学,求选出的两名同学恰好分别在两个图书馆学习且学习的次数和大于20的概率。
正确答案
见解析。
解析
知识点
正确答案
见解析。
解析
(1)设DQ=y,则x2+4xy=200,y=
S=4200x2+210×4xy+80×4×y2=38000+4000x2+
(2)S=38000+4000x2+


知识点
为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到如下图的2×2列联表。
则至少有 的把握认为喜爱打篮球与性别有关。
正确答案
解析
略
知识点
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示。
(1)估计这次测试数学成绩的平均分;
(2)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率。
正确答案
见解析。
解析
(1)利用组中值估算抽样学生的平均分:

=
=72
所以,估计这次考试的平均分是72分。┉┉┉┉┉┉┉┉5分
(2)从95,96,97,98,99,100中抽2个数的全部可能的基本结果有:
(95,96),(95,97),(95,98),(95,99),(95,100)
(96,97),(96,98),(96,99),(96,100)
(97,98),(97,99),(97,100),(98,99),(98,100),(99,100)
共15种结果。 ┉┉┉┉┉┉┉┉7分
如果这两个数恰好是两个学生的成绩,则这两个学生的成绩在[90,100]段,而[90,100]段的人数是0.005×10×80=4(人)┉┉┉┉┉┉┉┉8分
不妨设这4个人的成绩是95,96,97,98,则事件A=“2个数恰好是两个学生的成绩”,包括的基本结果有:(95,96),(95,97),(95,98),(96,97),(96,98),(97,98)共6种基本结果。 ┉┉┉┉┉┉┉┉10分
∴P(A)=
知识点
某厂对一批元件进行抽样检测。经统计,这批元件的长度数据 (单位:











正确答案
解析
略
知识点
设
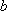
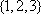
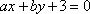
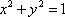
______,
正确答案
解析
略
知识点
某超市制定了一份“周日”促销活动方案,当天单张购物发票数额不低于100元的顾客可参加“摸球抽奖赢代金券”活动,规则如下:
①单张购物发票每满100元允许摸出一个小球,最多允许摸出三个小球(例如,若顾客购买了单张发票数额230元的商品,则需摸出两个小球);
②每位参加抽奖的顾客要求从装有1个红球,2个黄球,3个白球的箱子中一次性摸出允许摸出的所有小球;
③摸出一个红球获取25元代金券,摸出一个黄球获取15元代金券,摸出一个白球获取5元代金券。
已知活动当日小明购买了单张发票数额为338元商品,求小明参加抽奖活动时
(1)小明摸出的球中恰有两个是黄球的概率;
(2)小明获得代金券不低于30元的概率。
正确答案
见解析。
解析
知识点
为了均衡教育资源,加大对偏远地区的教育投入,调查了某地若予户家庭的年收入x(单位:万元)和年教育支出y(单位:万元),调查显示年收入x与年教育支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:
正确答案
0.15
解析
略
知识点
某商区停车场临时停车按时段收费,收费标准为:每辆汽车一次停车不超过

超过




(1)若甲停车





(2)若每人停车的时长在每个时段的可能性相同,求甲、乙二人停车付费之和为
正确答案
(1)
(2)
解析
(1)解:设“甲临时停车付费恰为


所以甲临时停车付费恰为

(2)解:设甲停车付费


则甲、乙二人的停车费用构成的基本事件空间为:


其中,

故“甲、乙二人停车付费之和为

知识点
一次考试结束后,随机抽查了某校高三(1)班5名同学的数学与物理成绩如下表:
(1)分别求这5名同学数学与物理成绩的平均分与方差,并估计该班数学与物理成绩那科更稳定;
(2)从以上5名同学中选2人参加一项活动,求选中的学生中至少有一个物理成绩高于90分的概率。
正确答案
见解析
解析
(1)5名学生数学成绩的平均分为:
5名学生数学成绩的方差为
5名学生物理成绩的平均分为:
5名学生物理成绩的方差为:
因为样本的数学成绩方差比物理成绩方差大,所以,估计高三(1)班总体物理成绩比数学成绩稳定。
(2)设选中的学生中至少有一个物理成绩高于90分为事件A,
5名学生中选2人包含基本事件有:A1A2,A1A3,A1A4,A1A5,A2A3,A2A4,A2A5,A3A4,A3A5,A4A5,共10个。
事件A包含基本事件有:A1A4,A1A5,A2A4,A2A5,A3A4,A3A5,A4A5,共7个.
所以,5名学生中选2人,选中的学生中至少有一个物理成绩高于90分的概率为
知识点
为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查,根据下图提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 ▲ 万只.
正确答案
90
解析
略
知识点
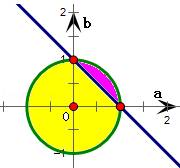
若实数a,b满足a2+b2≤1,则关于x的方程x2﹣2x+a+b=0无实数根的概率为( )
正确答案
解析
∵ 实数a,b满足a2+b2≤1,
∴ 以a为横坐标、b为纵坐标建立直角坐标系,可得所有的点(a,b)在以O为圆心,半径为1的圆及其内部,即单位圆及其内部,如图所示
若关于x的方程x2﹣2x+a+b=0无实数根,则满足△=4﹣4(a+b)<0,解之得a+b>1符合上式的点(a,b)在圆内且在直线a+b=1的上方,其面积为S1=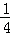
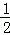
又∵ 单位圆的面积为S=π×12=π
∴ 关于x的方程x2﹣2x+a+b=0无实数根的概率为P=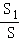
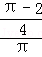
故选:D
知识点
一个总体分为甲、乙两层,用分层抽样方法从总体中抽取一个容量为

正确答案
180
解析
略
知识点
某种零件按质量标准分为1,2,3,4,5五个等级,现从一批该零件中随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
(1)在抽取的20个零件中,等级为5的恰有2个,求m,n;
(2)在(1)的条件下,从等级为3和5的所有零件中,任意抽取2个,求抽取的2个零件等级恰好相同的概率。
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析