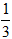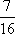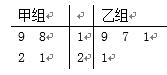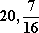- 概率与统计
- 共1335题
某医院为了支援汶川地震灾区的重建工作,要从4名男医生和3名女医生中选出3名医生前往灾区,至少有一男一女的不同选派方法有
正确答案
解析
至少一男一女包含一男二女和二男一女的情况,则选派数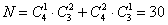
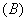
知识点
某班共有52人,现根据学生的学号,用系统抽样的方法,抽取一个容量为4的样本,已知3号、29号、42号同学在样本中,那么样本中还有一个同学的学号是
正确答案
解析
因为29号、42号的号码差为13,所以
知识点
为了解某市今年初二年级男生的身体素质状况,从该市初二年级男生中抽取了一部分学生进行“掷实心球”的项目测试.成绩低于6米为不合格,成绩在6至8米(含6米不含8米)的为及格,成绩在8米至12米(含8米和12米,假定该市初二学生掷实心球均不超过12米)为优秀,把获得的所有数据,分成
(1)求实数
(2)根据此次测试成绩的结果,试估计从该市初二年级男生中任意选取一人,“掷实心球”成绩为优秀的概率;
(3)若从此次测试成绩不合格的男生中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生来自不同组的概率。
正确答案
(1)40
(2)0.4
(3)
解析
(1)由题意可知

所以此次测试总人数为
答:此次参加“掷实心球”的项目测试的人数为40人, ……………………4分
(2)由图可知,参加此次“掷实心球”的项目测试的初二男生,成绩优秀的频率为

(3)设事件A:从此次测试成绩不合格的男生中随机抽取2名学生来自不同组。
由已知,测试成绩在



从这8人中随机抽取2人有

事件A包括
所以
答:随机抽取的2名学生来自不同组的概率为
知识点
某校为组建校篮球队,对报名同学进行定点投篮测试,规定每位同学最多投3次,每次在A或B处投篮,在A处投进一球得3分,在B处投进一球得2分,否则得0分,每次投篮结果相互独立,将得分逐次累加并用X表示,如果X的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮方案有以下两种:
方案1:先在A处投一球,以后都在B处投;
方案2:都在B处投篮.
已知甲同学在A处投篮的命中率为0.4,在B投投篮的命中率为0.6.
(1)甲同学若选择方案1,求X=2时的概率;
(2)甲同学若选择方案2,求X的分布列和期望;
(3)甲同学选择哪种方案通过测试的可能性更大?请说明理由.
正确答案
见解析。
解析
知识点
有一个不透明的袋子,装有3个完全相同的小球,球上分别编有数字l,2,3。
(1)若逐个不放回取球两次,求第一次取到球的编号为偶数且两个球的编号之和能被3整除的概率;
(2)若先从袋中随机取一个球,该球的编号为a,将球放回袋中,然后再从袋中随机取一个球,该球的编号为b,求直线ax+by+1=0与圆x2+ y2=
正确答案
见解析。
解析
知识点
在一次抽奖活动中,有a、b、c、d、e、f 共6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖。
(1)求a能获一等奖的概率;
(2)若a、b已获一等奖,求c能获奖的概率。
正确答案
(1)
(2)
解析
(1)设“a能获一等奖”为事件A,
事件A等价于事件“从6人中随机取抽两人,能抽到a”.从6人中随机抽取两人的基本事件有(a、b)、(a、c)、(a、d)、(a、e)、(a、f)、(b、c)、(b、d)、(b、e)、(b、f)、(c、d)、(c、e)、(c、f)、(d、e)、(d、f)、(e、f)15个, ………………4分
包含a的有5个,所以,P(A)=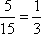
答: a能获一等奖的概率为
(2)设“若a、b已获一等奖,c能获奖”为事件B,
a、b已获一等奖,余下的四个人中,获奖的基本事件有(c,c)、(c、d)、(c、e)、(c、f)、(d,c)、(d、d)、(d、e)、(d、f)、(e,c)、(e、d)、(e、e)、(e、f)、(f,c)、(f、d)、(f、e)、(f、f)16个, ………………11分
其中含有c的有7种,所以,P(B)=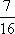
答: 若a、b已获一等奖,c能获奖的概率为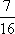
知识点
某公司有男职员45名,女职员15名,按照分层抽样的方法组建了一个4人的科研攻关小组。
(1)求某职员被抽到的概率及科研攻关小组中男、女职员的人数;
(2)经过一个月的学习、讨论,这个科研攻关组决定选出两名职员做某项实验,方法是先从小组里选出1名职员做实验,该职员做完后,再从小组内剩下的职员中选一名做实验,求选出的两名职员中恰有一名女职员的概率;
(3)试验结束后,第一次做试验的职员得到的试验数据为68,70,71,72,74,第二次做试验的职员得到的试验数据为69,70,70,72,74,请问哪位职员的实验更稳定?并说明理由。
正确答案
见解析。
解析
(1)

设有



(2)把







(3)

第二次做试验的职员做的实验更稳定………………………12分
知识点
我市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄(单位:岁)分组:第1组




(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参
加广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(2)请根据频率分布直方图,估计这100名志愿者样本的平均数;
(3)在(1)的条件下,该市决定在这6名志愿者中随机抽取2
名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率。
(参考数据:
正确答案
见解析。
解析
(1)第3组的人数为0.3×100=30, 第4组的人数为0.2×100=20, 第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:第3组:


所以应从第3,4,5组中分别抽取3人,2人,1人.
(2) 根据频率分布直方图,样本的平均数的估计值为:

所以,样本平均数为32.25岁.
(3) 记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1. 则从6名志愿者中抽取2名志愿者有:
(A1,A2), (A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),
(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:(A1,B1), (A1,B2), (A2,B1), (A2,B2), (A3,B1), (A3,B2), (B1,B2), (B1,C1), (B2,C1),共有9种
根据古典概型概率计算公式,得
答:第4组至少有一名志愿者被抽中的概率为
知识点
以下茎叶图记录了甲、乙两组各四名工人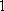
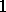
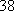
正确答案
解析
略
知识点
从





正确答案
解析
略
知识点
用计算机产生随机二元数组成区域






正确答案
解析
略
知识点
某校高一年级开设研究性学习课程,(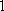
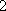
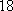
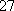
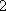
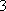
(1)求研究性学习小组的人数;
(2)规划在研究性学习的中、后期各安排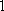
正确答案
(1)
(2)
解析
(1)解:设从(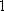
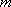
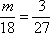
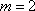
研究性学习小组的人数为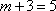
(2)设研究性学习小组中(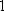
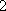
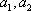
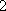
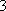
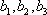
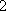
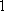
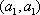
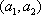
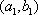
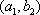
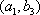
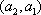
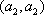
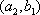
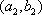
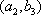
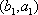
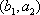
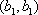
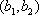
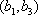
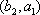
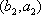
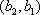
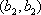
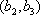
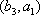
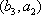
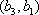
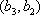
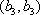
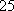
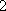
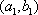
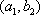
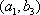
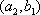
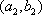
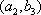
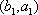
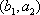
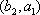
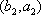
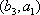
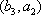
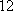
所以
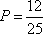
知识点
图(5)是某市2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择2月1日至2月12日中的某一天到达该市,并停留3天。
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率。
正确答案
见解析。
解析
(1)在2月1日至2月12日这12天中,只有5日、8日共2天的空气质量优良,所以此人到达当日空气质量优良的概率
(2)根据题意,事件“此人在该市停留期间至多有1天空气重度污染”,即“此人到达该市停留期间0天空气重度污染或仅有1天空气重度污染”
“此人在该市停留期间0天空气重度污染”等价于“此人到达该市的日期是4日或8日或9日”.其概率为
“此人在该市停留期间仅有1天空气重度污染”等价于“此人到达该市的日期是3日或5日或6日或7日或10日”.其概率为
所以此人停留期间至多有1天空气重度污染的概率为.P=
知识点








某城市环保局从该市市区


(1) 若从这

(2)根据这


正确答案
(1)
(2)
解析
由茎叶图可知:6天有4天空气质量未超标,有2天空气质量超标………2分
记未超标的4天为


基本事件总数为15 ……………………………………………………4分
(1)记“至多有一天空气质量超标”为事件

易得

(2)


所以估计一年中平均有
(说明:答243天,244天不扣分)
知识点
一个质地均匀的正方体的六个面上分别标有数字



(1)求事件
(2)求事件“点

正确答案
(1)
(2)
解析
(1)由题可知


基本事件空间:
共计24个基本事件 ……………………3分
满足

所以事件

(2)设事件B=“点(a,b)满足
当

当

当

所以满足

所以
知识点
扫码查看完整答案与解析