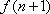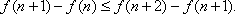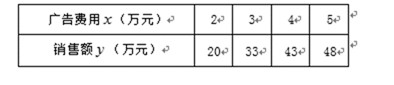- 概率与统计
- 共1335题
将容量为
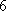
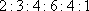
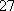

正确答案
60
解析
略
知识点
某容量为180的样本的频率分布直方图共有



正确答案
解析
略
知识点
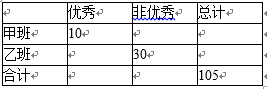
有甲乙两个班进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下列联表。
已知在全部105人中随机抽取1人为优秀的概率为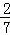
(1)请完成上面的联表;
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班10优秀的学生按2到11进行编号,先后两次抛掷一枚骰子,出现的点数之和为被抽取的序号,试求抽到6号或10号的概率。
参考公式:K2=
概率表
正确答案
见解析。
解析
(1)
(2)根据列联表中的数据,得到k2=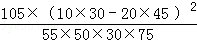
因此有95%的把握认为“成绩与班级有关系”。
(3)设“抽到6或10号”为事件A,先后两次抛掷一枚均匀的骰子,出现的点数为(x,y)。
所有的基本事件有(1,1)、(1,2)、(1,3)、(6,6),共36个。
事件A包含的基本事件有:(1,5)、(2,4)、(3,3)、(4,2)、(5,1)(4,6)、(5,5)、(6、4),共8个
∴P(A)=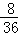
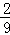
知识点
如图为某个容量为100的样本的频率分布直方图,分组为

正确答案
解析
略
知识点
将一个正整数
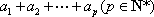
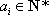
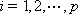
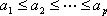
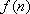
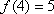
(1)写出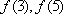
(2)证明: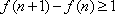
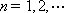
(3)对任意正整数
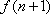
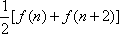
正确答案
见解析
解析
(1)解:因为3=3,3=1+2,3=1+1+1,所以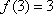
因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1,
所以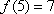
(2)证明:因为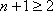
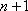
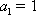
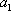


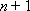
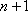
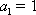

所以 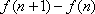
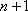
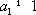
即 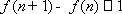
(3)结论是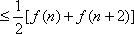
证明如下:由结论知,只需证
由(2)知: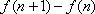

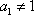
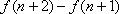
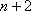
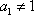
考虑到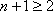
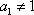
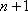
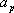
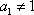
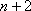
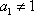
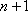
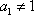
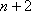
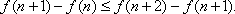
知识点
某校为了研究学生的性别和对待某一活动的态度(支持与不支持)的关系,运用2
附:
正确答案
解析
略
知识点
已知函数


在其取值范围内任取实数


上为增函数的概率为
正确答案
解析
略
知识点
某产品的广告费用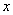
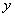
根据上表数据用最小二乘法求得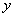
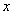
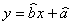
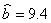
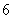
正确答案
59.5万元
解析
略
知识点
某高校在2012年的自主招生考试成绩中随机抽以100名学生的

(1)为了能选拔出最优秀的学生,该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进

(2)在(1)的前提下,学校决定在

正确答案
见解析。
解析
(1)
由图得,第3组的频率为0.3,故频数为30,第四组的频率为0.2,故频数为20,第5组的频率为0.1,故频数为10。因为第3,4,5组共有60组学生,所以利用分层抽样在60组学生中抽取6名学生,每组分别为
(2)
知识点
一个盒子中装有





(1)若一次抽取


(2)若第一次抽


正确答案
见解析。
解析
(1)设






其中数字之和大于


所以
(2)设

第一次抽1张,放回后再抽取一张卡片的基本结果有:


事件

共
所以所求事件的概率为
知识点
某中学共有学生2000人,各年级男、女生人数如下表:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(3)已知

正确答案
见解析。
解析
(1)由 

(2)高三年级人数为
现用分层抽样的方法在全校抽取48名学生,应在高三年级抽取的人数为
(3)设高三年级女生比男生多的事件为A,高三年级女生、男生数记为
(2)知



知识点
某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为



(1)每套丛书售价定为100元时,书商能获得的总利润是多少万元?
(2)每套丛书售价定为多少元时,单套丛书的利润最大?
正确答案
见解析。
解析
(1)每套丛书售价定为100元时,销售量为
此时每套供货价格为
书商所获得的总利润为
(2)每套丛书售价定为


依题意,单套丛书利润
∴
∵ 
∴ 
由 
当且仅当


知识点
从


正确答案
解析
略
知识点
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示),若在


正确答案

解析
略
知识点
对某校全体教师在教学中是否经常使用信息技术实施教学的情况进行了调查,得到统计数据如下:
(1)求该校教师在教学中不经常使用信息技术实施教学的概率;
(2)在教龄


正确答案
(1)
(2)
解析
(1)解:该校教师人数为

设“该校教师在教学中经常使用信息技术实施教学”为事件
则

所以该校教师在教学中不经常使用信息技术实施教学的概率是
(2)解:设经常使用信息技术实施教学,教龄在





















设“任选


包括的基本事件为







则
所以恰有一人教龄在

知识点
扫码查看完整答案与解析