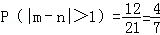- 概率与统计
- 共1335题
科学研究表明:一般情况下,在一节40分钟的课中,学生的注意力随教师讲课的时间变化而变化。开始上课时,学生的注意力逐步增强,随后学生的注意力开始分散。经过实验分析,得出学生的注意力指数

(1)如果学生的注意力指数不低于80,称为“理想听课状态”,则在一节40分钟的课中学生处于“理想听课状态”所持续的时间有多长?(精确到1分钟)
(2)现有一道数学压轴题,教师必须持续讲解24分钟,为了使效果更好,要求学生的注意力指数在这24分钟内的最低值达到最大,那么,教师上课后从第几分钟开始讲解这道题?(精确到1分钟)
正确答案
(1)

解析
解析:(1)由于学生的注意力指数不低于80,即
当


当


所以
故学生处于“理想听课状态”所持续的时间有
(2)设教师上课后从第
所以
要学生的注意力指数最低值达到最大,只需
即
解得
所以,教师上课后从第
知识点
某年某省有








(1)请估计该次高考成绩在

(2)考生A填报志愿后,得知另外有4名同分数考生也填报了该志愿。若该志愿计划录取2人,并在同分数考生中随机录取,求考生A被该志愿录取的概率。
正确答案
见解析。
解析
(1)由所给的数据估计该年广东省文科考生成绩在
(2)设另外4名考生分别为







知识点
高三(1)班的一个研究性学习小组在网上查知,某珍稀植物种子在一定条件下发芽成功的概率为
(1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验恰好有3次成功的概率;
(2)若两小组都做4次试验(每次均种下一粒种子),求第二小组比第一小组多成功3次的概率;
正确答案
见解析。
解析
(1)该事件为5次独立重复试验发生3次
∴P=P5(3)
=
(2)
分布列如下:
∴ E
知识点
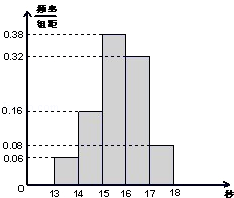
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图。
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)设m,n表示该班某两位同学的百米测试成绩,且已知m,n∈[13,14)∪[17,18],求事件“|m﹣n|>1”的概率。
正确答案
见解析。
解析
(1)由直方图知,成绩在[14,16)内的人数为:50×0.16+50×0.38=27(人),
所以该班成绩良好的人数为27人、
(2)由直方图知,成绩在[13,14)的人数为50×0.06=3人,
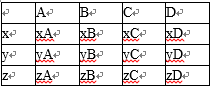
设为为x,y,z;成绩在[17,18]的人数为50×0,08=4人,设为A、B、C、D。
若m,n∈[13,14)时,有xy,xz,yz共3种情况;
若m,n∈[17,18]时,有AB,AC,AD,BC,BD,CD,共6种情况;
若m,n分别在[13,14)和[17,18]内时,
有12种情况、
所以,基本事件总数为3+6+12=21种,事件“|m﹣n|>1”所包含的基本事件个数有12种、
∴
知识点
从甲,乙,丙,丁4个人中随机选取两人,则甲乙两人中有且只一个被选取的概率为 。
正确答案
解析
从甲,乙,丙,丁4个人中随机选取两人,共有(甲乙),(甲丙),(甲丁),(乙丙),(乙丁),(丙丁)六种,
其中甲乙两人中有且只一个被选取,则(甲丙),(甲丁),(乙丙),(乙丁),共4种,
故甲乙两人中有且只一个被选取的概率为
知识点
将甲、乙两个球随机放入编号为1,2,3的3个盒子中,每个盒子的放球数量不限,则在1,2号盒子中各有1个球的概率为 .
正确答案
解析
甲球有三种放法,乙球也有三种放法,共有9种放法,在1,2号盒子中各有1个球的放法有2种,所概率为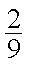
知识点
某校一个甲类班x名学生在2011年某次数学测试中,成绩全部介于90分与140分之间,将测试结果按如下方式分成五组,第一组


(1)求x及分布表中m,n,t的值;
(2)设a,b是从第一组或第五组中任意抽取的两名学生的数学测试成绩,求事件“
正确答案
见解析。
解析
(1)
(2)第一组
第五组
则

记“



∴
∴事件“

知识点
某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组【13,14),第二组【14,15),…,第五组【17,19),下图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽一个同学组成一个新的组,求这个新组恰好由一个男生和一个女生构成的概率.
正确答案
见解析。
解析
(1)由频率分布直方图知,成绩在第一组的为优秀,频率为0.06,
人数为:50×0.06=3
所以该样本中成绩优秀的人数为3。
(2)由频率分布直方图知,成绩在第三组的频率0.38,以此估计本年级900名学生成绩属于第三组的概率为0.38,
人数为:900×0.38=342
所以估计本年级900名学生中,成绩属于第三组的人数为342。
(3)样本中第一组共有3人,
由第五组的频率为0.08,可得第五组共有4人。
其中第五组四人记为



所以基本事件有12个
恰为一男一女的事件有1b,1c,1d,2b,2c,2d,3a;共7个
因此新组恰由一男一女构成的概率是
知识点
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆。
(1)求z的值;
(2)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2. 把这8辆轿车的得分看作一个总体,从中任取一个分数





正确答案
见解析。
解析
(1)设该厂本月生产轿车为



(2)8辆轿车的得分的平均数为
…………………………………………6分
把8辆轿车的得分看作一个总体,从中任取一个分数

由





知识点
袋中装有2个红球,2个白球,除颜色外其余均相同,现从中任意摸出2个小球,则摸出的两球颜色不同的概率为 。
正确答案

解析
从袋中任意地同时摸出两个球共


故其概率是


故答案为:
知识点
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示。
(1)根据图中的数据信息,求出众数

(2)小明的父亲上班离家的时间



正确答案
见解析
解析
(1)
由频率分布直方图可知

∴
解得

设报纸送达时间为
则小明父亲上班前能取到报纸等价于 
如图可知,所求概率为
知识点
某学校有两个食堂,甲、乙、丙三名学生各自随机选择其中的一个食堂用餐,则他们在同一个食堂用餐的概率为___▲__。
正确答案
解析
因甲、乙、丙三名学生在两个食堂中选一个用餐,共有

知识点
已知点


正确答案
解析
“劣弧

知识点
某射击选手连续射击5枪命中的环数分别为:9.7,9.9,10.1,10.2,10.1,则这组数据的方差为 。
正确答案
0.032。
解析
解:数据9.7,9.9,10.1,10.2,10.1的平均数=
方差=
知识点
在面积为1的正方形



正确答案
解析
由题意知本题是一个等可能事件的概率,以





知识点
扫码查看完整答案与解析