- 概率与统计
- 共1335题
豌豆的高矮性状的遗传由其一对基因决定,其中决定高的基因记为D,决定矮的基因记为d,
则杂交所得第一子代的一对基因为Dd,若第二子代的D,d的基因遗传是等可能的(只要有基
因D则其就是高茎,只有两个基因全是d时,才显示矮茎),则第二子代为高茎的概率为 ▲ 。
正确答案
解析
第二子代的一对基因的所有等可能情形为DD,Dd,dD,dd,其中高茎的有DD,Dd,dD共3种,则所求概率为
知识点
某县为增强市民的环境保护意识,面向全县征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组




(1)分别求第3,4,5组的频率.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传
经验,求第4组至少有一名志愿者被抽中的概率.
正确答案
见解析。
解析
(1) 由题设可知,第3组的频率为0.06×5=0.3,
第4组的频率为0.04×5=0.2,
第5组的频率为0.
(2)第3组的人数为0.3×
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:
第3组:


所以应从第3,4,5组中分别抽取3人,2
(3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1.
则从6名志愿者中抽取2名志愿者有:
(A1,A2), (A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),
(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1), (A1,B2), (A2,B1), (A2,B2), (A3,B1), (A3,B2), (B1,B2), (B1,C1), (B2,C1
所以第4组至少有一名志愿者被抽中的概率为
知识点
继“三鹿奶粉”,“瘦肉精”, “地沟油”等事件的发生之后,食品安全问题屡屡发生,引起了国务院的高度重视.为了加强食品的安全,某食品安检部门调查一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的重量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长的速度为1.0~1.2kg/年的比重超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题。
(1)根据数据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否存在问题?
(2)上面捕捞的100条鱼中间,从重量在



正确答案
见解析。
解析
(1)捕捞的100条鱼中间,数据落在

数据落在

所以数据落在[1.20,1.30)中的概率约为
由于


故饲养的这批鱼没有问题. (6分)
(2)重量在
重量在


而恰好所取得鱼重量在


所以恰好所取得鱼重量在


知识点
在集合
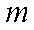




正确答案
解析
由题意得到的
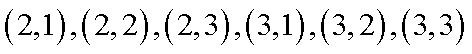


知识点
某校为了解学生的睡觉情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用下面的条形图表示,根据条形图可得这50名学生这一天平均每人的睡眠时间为_______________
正确答案

解析

知识点
已知数字发生器每次等可能地输出数字1或2中的一个数字,则连续输出的4个数字之和能被3整除的概率是 。
正确答案
解析
由题意知本题是一个古典概型,
∵ 试验发生包含的事件是连续输出的4个数字,
每次等可能地输出数字1或2中的一个数字,
则有2×2×2×2=16,共有16种结果,
满足条件的事件是连续输出的4个数字之和能被3整除,即连续输出的4个数字中有两个1和两个2,表示为1,1,2,2;1,2,1,2;1,2,2,1;2,1,1,2;2,2,1,1;2,1,2,1。
可知有6种结果,
∴ 根据古典概型概率公式得到P=

故答案为:
知识点
在一本书中,分组统计100个句子中的字数,得出下列结果:字数1~5个的5句,字数6~10个的27句,字数11~15个的32句,字数16~20个的21句,字数21~25个的9句,字数26~30
个的6句,利用组中值可估计该书中平均每个句子所包含的字数为 ▲ 。
正确答案
14
解析
利用组中值得平均每个句子所包含的字数为
知识点
为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如图所示,则该组数据的方差为 .
正确答案
5
解析
平均数
故方差
知识点
若在区间





正确答案
解析
由题意知
直线


∴阴影梯形的面积为
而区间


知识点
在数轴上区间


正确答案
解析



知识点
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率,
正确答案
见解析。
解析
(1)①②位置的数据分别为12、0.3;
(2) 第三、四、五组参加考核人数分别为3、2、1;
(3)设上述6人为abcdef(其中第四组的两人分别为d,e),则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}共有15种,
记“2人中至少有一名是第四组”为事件A,则事件A所含的基本事件的种数有9种,
所以

知识点
某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求ξ的分布及数学期望;
(2)记“函数f(x)=x2﹣3ξx+1在区间[2,+∞)上单调递增”为事件A,求事件A的概率。
正确答案
见解析
解析
(1)分别记“客人游览甲景点”,“客人游览乙景点”,“客人游览丙景点”
为事件A1,A2,A3。
由已知A1,A2,A3相互独立,P(A1)=0.4,P(A2)=0.5,P(A3)=0.6。
客人游览的景点数的可能取值为0,1,2,3.相应地,客人没有游览的景点数的可能取值
为3,2,1,0,所以ξ的可能取值为1,3。
P(ξ=3)=P(A1•A2•A3)+P(
=P(A1)P(A2)P(A3)+P(
=2×0.4×0.5×0.6=0.24,
P(ξ=1)=1﹣0.24=0.76。
所以ξ的分布列为
Eξ=1×0.76+3×0.24=1.48。
(2)因为
所以函数
要使f(x)在[2,+∞)上单调递增,当且仅当
从而
知识点
已知某种从太空飞船中带回的植物种子每粒成功发芽的概率都为
(1)第一小组做了三次实验,求至少两次实验成功的概率;
(2)第二小组进行试验,到成功了4次为止,求在第四次成功之前共有三次失败,且恰有两次连续失败的概率。
正确答案
见解析
解析
(1)第一小组做了三次实验,至少两次实验成功的概率是
(2)第二小组在第4次成功前,共进行了6次试验,其中三次成功三次失败,且恰有两次连续失败,就是3次成功试验的间隔4空中选2个空,一个空位放置2次连续失败,一个放置一次失败,
其各种可能的情况种数为

因此所求的概率为
知识点
某产品按行业生产标准分成








3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数


(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率。
正确答案
见解析
解析
解析:(1)由样本数据知,30件产品中,一等品有6件,二等品有9件,三等品有15件. …………3分
∴样本中一等品的频率为
故估计该厂生产的产品的一等品率为
二等品的频率为

三等品的频率为

(2)样本中一等品有6件,其中等级系数为7的有3件,等级系数为8的也有3件, ……………………7分
记等级系数为7的3件产品分别为


















记从“一等品中随机抽取2件,2件等级系数都是8”为事件
则

故所求的概率
知识点
在长为




正确答案
解析
设




知识点
扫码查看完整答案与解析


























