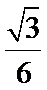空间向量的数量积运算
共5题

· 空间向量的数量积运算

空间向量的数量积运算
共5题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 6 分

15.已知是空间单位向量，，若空间向量满足，且对于任意x，y∈R，，则＝，＝，＝．

正确答案

1；2；；

解析

试题分析：利用向量模的平方及取到的最小值进行转化，求出值即可。

∵，∴当且仅当时取得最小值1，两边平方可得在时取到最小值1，＝，

∴。

考查方向

本题主要考查了空间向量的数量积的性质，向量的模，属于中等题．

解题思路

根据空间向量的模的平方等于向量数量积的平方，由向量模的最小值进行转

化，利用取得最小值时的条件求解．

易错点

空间向量模的平方的运算.

知识点

空间向量的数量积运算向量的数量积判断向量的共线与垂直空间直线的向量参数方程

题型：填空题

填空题 · 5 分

16．如图，在三棱锥中，已知，，设，

则的最小值为 .

正确答案

解析

因为

,所以，所以=，当且仅当时等号成立。

考查方向

本题主要考查向量数量积的运算以及向量的加减法和基本不等式求最值。

解题思路

1)利用向量的加减法将已知向量转化；

2)将向量关系转化为边的关系。

易错点

本题不能将空间的向量问题转化为边角之间的关系解决问题。

知识点

空间向量的数量积运算与二面角有关的立体几何综合题

题型：简答题

简答题 · 12 分

如图，四边形ABCD中，AB⊥AD，AD∥BC，AD＝3，BC＝2AB＝2，E，F分别在BC，AD上，EF∥AB．现将四边形ABEF沿EF折起，使平面ABEF⊥平面EFDC．

20.若，在折叠后的线段上是否存在一点，且，

使得∥平面ABEF?若存在，求出λ的值；若不存在，说明理由；

21.求三棱锥A－CDF的体积的最大值，并求此时二面角E－AC－F的余弦值．

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

（Ⅰ）因为平面平面，平面∩平面,

所以平面，又平面,

所以

在折起过程中，,同时∩，

所以平面

以为坐标原点，分别以所在直线为轴，建立如图所示的空间直角坐标系.

若时，则各点坐标如下：，, , .

可得平面的法向量．

因为，所以

所以,

故.

则,解得.

所以线段上存在一点，且，使得∥平面ABEF.

考查方向

本题主要考查空间线面平行与垂直的判定与性质，几何体的体积，二面角等知识，意在考查考生的空间想象能力和运算求解能力.

解题思路

先根据题中给出的条件证明平面，然后建立空间直角坐标系求解即可；

易错点

1.不知道折叠前后变的量和不变的量有哪些?2.不会根据题中的条件找到建立坐标系的条件。

第(2)小题正确答案及相关解析

正确答案

（2）

解析

（Ⅱ）设，所以，,

所以，

所以当时，有最大值，且最大值为.

可得, , ，.

所以,,,.

设平面的一个法向量为,

则,即.

取，则,

设平面的一个法向量为,

则，即

同理可得

所以

所以二面角E﹣AC﹣F的余弦值为.

考查方向

本题主要考查空间线面平行与垂直的判定与性质，几何体的体积，二面角等知识，意在考查考生的空间想象能力和运算求解能力.

解题思路

设出变量后得到函数，然后求其最大值后得到想x的值，然后按照空间向量的知识求解即可。

易错点

1.不知道折叠前后变的量和不变的量有哪些?2.不会根据题中的条件找到建立坐标系的条件。

题型：填空题

填空题 · 5 分

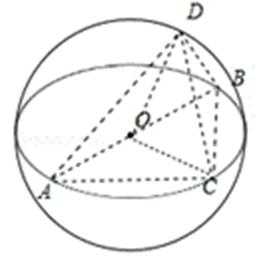
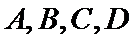
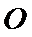
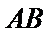
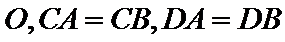
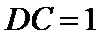
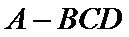
15.半径为1的球面上有四个点，球心为点，过点，，则三棱锥的体积为_____________.

正确答案

解析

由题意可知图形如图所示，

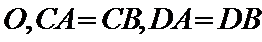
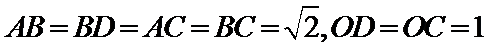
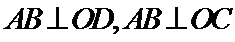
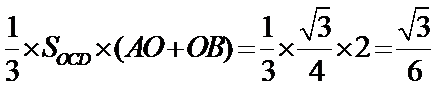
AB过点，三角形ABD与三角形ACB都是等腰直角三角形，且，，几何体的体积为。

考查方向

本题主要考查了空间几何体的体积问题，主要考查了“分割法”求体积的思想。

解题思路

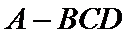
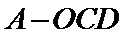
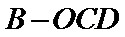
根据图中的有关关系，确定图形的特征，将三棱锥分割为和即可很容易地求解。

易错点

本题容易因对球面上的问题想象不到位，不能很好地寻求分割图形的策略而导致错误的出现。

知识点

空间向量的数量积运算

题型：简答题

简答题 · 14 分

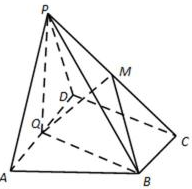
18．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD//BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC上的点，PA=PD=2，BC=AD=1，CD=．

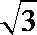
（1）若点M是棱PC的中点，求证：PA // 平面BMQ；

（2）求证：平面PQB⊥平面PAD；

（3）若二面角M-BQ-C为30°，设PM=tMC，试确定t的值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间向量的数量积运算

棒棒哒，已学完当前知识点学习下一知识点

下一知识点 : 空间向量的夹角与距离求解公式

百度题库 > 高考 > 理科数学 > 空间向量的数量积运算

扫码查看完整答案与解析