- 二次函数的零点问题
- 共17题
8.已知:关于x的方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设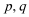
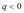
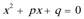
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数

(1)当
(2)当
(3)当
(4)当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知开口向上的二次函数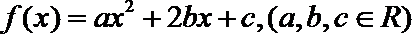
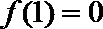
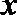
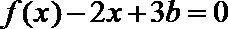
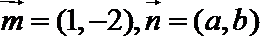
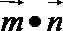

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知二次函数



(1)求
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数f(x)=x2-ax+2在区间[0,1]上至少有一个零点,则实数a的取值范围是__________.
正确答案
[3,+∞)
解析
由题意,
知关于x的方程x2-ax+2=0在区间[0,1]上有实数解.
又x=0不是方程x2-ax+2=0的解,
所以根据0<x≤1
可将方程x2-ax+2=0变形为
从而问题转化为求函数
因为函数g(x)在(0,1]上单调递减,
所以g(x)∈[3,+∞).
故所求实数a的取值范围是[3,+∞)。
知识点
10.若方程x2-4|x|+5-m=0恰有4个不同的实数解,则实数m的取值范围是 .
正确答案
(1,5)
解析
设函数
函数y2=m,则方程x2-4|x|+5=m的实数解就是函数y1与y2图象交点的横坐标,
当方程x2-4|x|+5=m有4个不同的实数解时,
两个函数的图象应有4个不同的交点,
在同一直角坐标系中作出两个函数的图象,
如图所示,
则可得实数m的取值范围是(1,5).
知识点
阅读下面材料:
根据两角和与差的正弦公式,有

由①+②得
令
代入③得 
(1)类比上述推理方法,根据两角和与差的余弦公式,证明:

(2)若



正确答案
见解析。
解析
解法一:(1)证明:因为

①-② 得
令

代入③得
(2)由二倍角公式,

所以
设

由正弦定理可得
根据勾股定理的逆定理知
解法二:(1)同解法一。
(2)利用(1)中的结论和二倍角公式,

因为A,B,C为

所以
又因为

所以
从而
又


所以
知识点
若关于





(1)设

(2)过点





正确答案
(1)
解析
解析:方程








内,点

易得图中

(1)令






又

(2)过点


可能满足条件的整点为



知识点
16.已知


(1)求
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析