- 圆方程的综合应用
- 共21题
10.如图,在圆的内接四边形





正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
在△
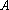

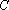

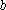


(1)求角A的大小;
(2)若△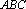

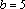

正确答案
(1)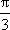
解析
(1)由cos 2A-3cos(B+C)=1,
得2cos2A+3cos A-2=0,
即(2cos A-1)(cos A+2)=0,
解得cos A=
因为0<A<π,所以A=
(2)由S=

由余弦定理得a2=b2+c2-2bccos A=25+16-20=21,故
又由正弦定理得sin Bsin C=
知识点
已知平面




正确答案
解析
作示意图如,由圆M的面积为4





故选D
知识点
在直角坐标系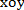
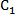
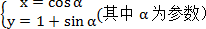
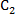
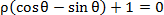
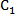
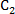
正确答案
2
解析
曲线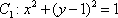
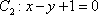
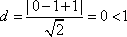

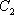
知识点
已知点A,B分别为椭圆:



(1)求椭圆方程;
(2)若椭圆上存在点P,满足

(3)在(2)的条件下,当
正确答案
见解析。
解析
知识点
变量



仅在点

正确答案
解析
略
知识点
由直线

正确答案
解析
略
知识点
如图,在△ABC中,∠C=90°,∠A=60°,AB=20,过C作△ABC的外接圆的切线CD,BD⊥CD,BD与外接圆交于点E,则DE的长为__________。
正确答案
5
解析
在Rt△ABC中,∠A=60°,AB=20,可得BC=
由弦切角定理,可得∠BCD=∠A=60°。
在Rt△BCD中,可求得CD=
又由切割线定理,可得CD2=DE·DB,可求得DE=5
知识点
已知一元二次不等式f(x)<0的解集为
正确答案
解析
由题意知-1<10x<
所以x<
知识点
已知有限集


①集合
②

③
④若

其中正确的结论是___________.(填上你认为所有正确的结论序号)
正确答案
①③④
解析
易判断①是正确的;
②不妨设a1+a2=a1a2=t,则由韦达定理知a1,a2是一元二次方程x2-tx+t=0的两个根,由Δ>0,可得t<0,或t>4,故②错;
③不妨设A中a1<a2<a3<…<an,由a1a2…an=a1+a2+…+an<nan,得

知识点
扫码查看完整答案与解析















