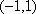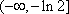- 圆方程的综合应用
- 共21题
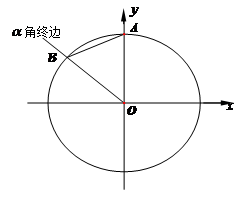
13.已知圆x2+y
正确答案
-4
解析
圆的标准方程为:

考查方向
解题思路
把圆的方程转化为标准形式,求出弦心距,再由条件根据弦长公式求得a的值
易错点
计算错误
知识点
7.已知圆








正确答案
解析
圆C








考查方向
解题思路
1.先求出圆

易错点
圆

知识点
8.已知直线l:x+ay-1=0(a

正确答案
解析
圆



因此



考查方向
解题思路
首先圆是一个对称图形,它关于圆心成中心对称,关于每一条直径所在直线都是它的对称轴,当然其对称轴一定过圆心,其次直线与圆有相交、相切、相离三种位置关系,判断方法可用几何与代数两种方法研究,圆的切线长我们用勾股定理求解,设圆外一点




易错点
求解参数a
知识点
12.已知直线



正确答案
解析
由已知得圆心到直线的距离小于半径,即
【或由
所以
由

如图,又由
因



考查方向
解题思路
1.先根据直线


易错点
不会转化题中向量的条件,导致无法做出正确答案。
知识点
人民警察有下列情形之一,经批评教育、纪律处分仍不改正的,或者经培训试用后仍不合格的,应当予以辞退:( )。
A.耍特权,态度恶劣,刁难辱骂群众,侵犯公民合法权益的
B.经常喝酒的
C.文化、业务素质低,不适应公安工作的
D.对遇有危难情形的群众拒绝提供救助的
正确答案
A,C,D
解析
[解析] 《公安机关人民警察辞退办法》第四条规定:人民警察有下列情形之一,经批评教育、纪律处分仍不改正的,或者经培训试用后仍不合格的,应当予以辞退:①作风散漫,纪律松弛,经常迟到、早退或者上班时间经常办私事的;②遇事推诿,消极怠工,工作不负责任的;③耍特权,态度恶劣,刁难辱骂群众,侵犯公民合法权益的;④酗酒滋事或者经常酗酒的;⑤私自将警械、警服、警衔标志转借、赠送非人民警察的;⑥不按规定着装,警容不严整,举止不端庄的;⑦对遇有危难情形的群众拒绝提供救助的;⑧文化、业务素质低,不适应公安工作的。故选ACD。

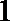
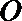
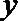
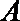
钝角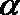
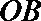
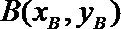
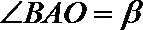
(1)用
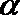
(2)如果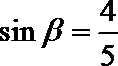
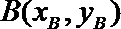
(3)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.选修4—1:
如图,直线AB经过圆O上的点C,并且OA=OB,CA=CB,圆O交直线OB于点E、D,其中D在线段OB上.连结EC,CD.
(Ⅰ)证明:直线AB是圆O的切线;
(Ⅱ)若tan∠CED=
正确答案
(1)略;
(2)5.
解析
解题过程如下:
(1)证明:连结






(2)因为直线



则有


设




解得

考查方向
解题思路
本题考查几何证明选讲的相关知识,解题步骤如下: 1、根据图形做辅助线,利用切线的判定定理即可证明。2、利用切割弦定理解决长度的问题。
易错点
试题分析:本题属于几何证明选讲中的基本问题,题目的难度一般
知识点
15.已知P,A,B,C是球O球面上的四点,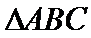
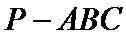
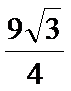
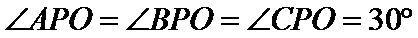
正确答案
解析
由
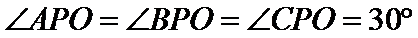
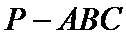
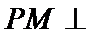
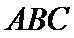
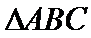
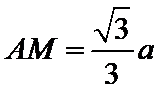
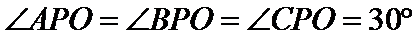
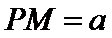
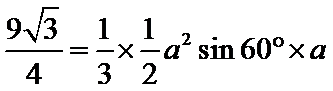
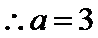

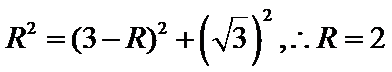
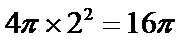
考查方向
解题思路
1.先根据条件判断出三棱锥为正三棱锥,根据体积求出底面边长和高;
2.将球心和半径所在的平面提出来, 利用平面几何的知识求解。
易错点
1.无法根据条件判断出三棱锥为正三棱锥;
2.不能确定球心O所在位置
知识点
7. 直线




则“


(填写“充分不必要”、“必要不充分”、“充要”、“既不充分又不必要”之一)
正确答案
充分而不必要
解析
由直线






考查方向
充分条件、必要条件、充要条件的判断
解题思路
根据题意和相关性质,分别求出两个命题,然后进行判断
易错点
化简错误
知识点
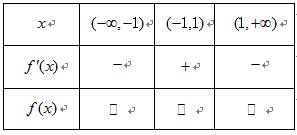
已知函数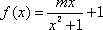
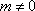
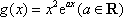
(1)求函数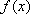
(2)当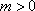
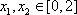
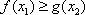

正确答案
(1)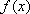
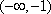
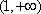
(2)
解析
(1)函数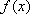
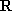
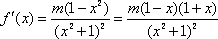
① 当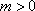

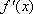

所以,函数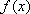
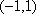
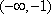
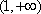
…………3分
② 当

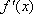
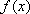
所以,函数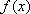
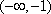
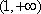
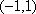
(2)依题意,“当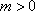
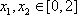
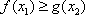
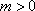
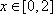
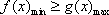
当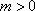
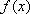
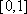
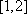
因为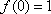
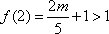
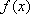
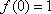
所以应满足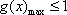
因为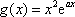
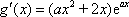
①当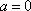
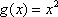
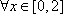
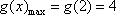
显然不满足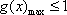
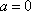
②当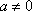
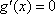
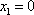
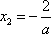
(ⅰ)当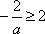
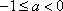
在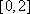
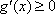
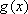
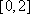
所以函数
由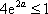
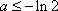
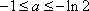
(ⅱ)当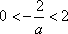
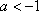
在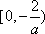
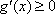
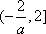
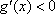
所以函数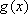
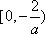
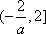
所以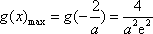
由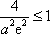
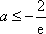
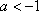
(ⅲ)当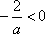
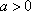
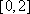
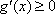
函数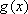
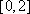
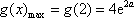
显然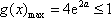
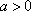
综上所述,
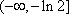
知识点
扫码查看完整答案与解析