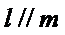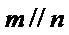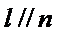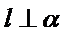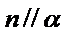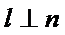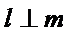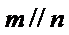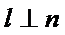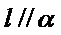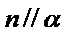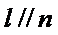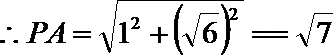- 直线与平面垂直的判定与性质
- 共169题
15.已知直线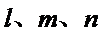
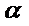
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在如图所示的几何体中,平面






(1)求证:

(2)求二面角
正确答案
(1)∵平面





又
且


(2)(解法一)建立如图空间直角坐标系
不妨设
则由题意得


设平面



设平面



所以
∴二面角

(解法二)取


因为

∴






则


由题意,不妨设
连接

因此在



因此二面角
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,AD

(1)求证:AF∥平面BDE;
(2)求证:平面BDE
正确答案
(1)证明:∵AD⊥平面ABC,AC

∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.
∴凸多面体ABCED的体积
求得CE=2.
取BE的中点G,连结GF,GD,
则GF∥EC,GF
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.
又∵GD

∴AF∥平面BDE.
(2)证明:∵AB=AC,F为BC的中点,
∴AF⊥BC.
由(1)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF,∴DG⊥面BCE.
∵DG
解析
解析已在路上飞奔,马上就到!
知识点
3.若A为
①



正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
19.已知在正四棱锥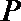


正确答案
设底边长为
故
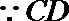
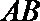



所以,异面直线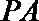

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析