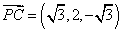- 直线与平面垂直的判定与性质
- 共169题
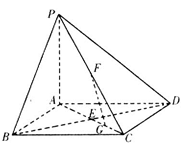
如图,在底面是正方形的四棱锥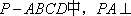
(1)求证: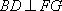
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由;
(3)当二面角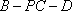
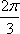
正确答案
见解析
解析
知识点
设m,n是两条不同的直线,

正确答案
解析
略
知识点
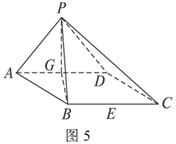
如图5,在四棱锥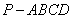
2的菱形,且DAB=60. 侧面PAD为正三角形,其所在的平
面垂直于底面ABCD,G为AD边的中点.
(1)求证:BG平面PAD;
(2)求平面PBG与平面PCD所成二面角的平面角的余弦值;
(3)若E为BC边的中点,能否在棱PC上找到一点F,使平面DEF平面ABCD,并证明你的结论.
正确答案
见解析。
解析
(1)证明:连结BD.
因为ABCD为棱形,且∠DAB=60°,所以ABD为正三角形.
又G为AD的中点,所以BG⊥AD.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴BG⊥平面PAD.
(2)∵△PAD为正三角形,G为AD的中点,∴PG⊥AD.
∵PG平面PAD,由(1)可得:PG⊥GB. 又由(1)知BG⊥AD.
∴PG、BG、AD两两垂直.
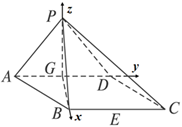
故以G为原点,建立如图所示空间直角坐标系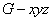
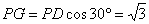
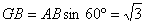
所以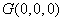
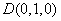
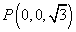
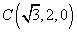
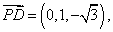
设平面PCD的法向量为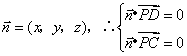
令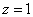
又平面PBG的法向量可为
设平面PBG与平面PCD所成二面角的平面角为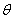
∴
即平面PBG与平面PCD所成二面角的平面角的余弦值为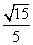
(3)当F为PC的中点时,平面DEF⊥平面ABCD.
取PC的中点F,连结DE,EF,DF,CG,且DE与CG相交于H.
因为E、G分别为BC、AD的中点,所以四边形CDGE为平行四边形,
故H为CG的中点. 又F为CP的中点,所以FH//PG.
由(2),得PG平面ABCD,所以FH平面ABCD.
又FH平面DEF,所以平面DEF⊥平面ABCD.
知识点
等边三角形ABC的边长为3,点D、E分别是边AB、AC上的点,且满足




(1)求证:
(2)在线段BC上是否存在点P,使直线


正确答案
见解析
解析
知识点
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿直线BD将△BCD翻折成△B

(1)求证:
(2)求直线BD与平面
正确答案
见解析。
解析
知识点
扫码查看完整答案与解析