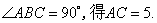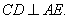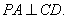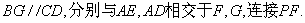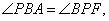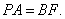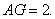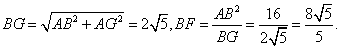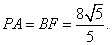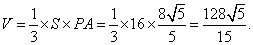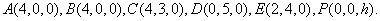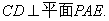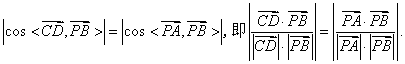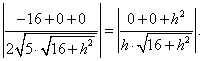- 直线与平面垂直的判定与性质
- 共169题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
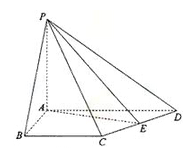
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
正确答案
见解析。
解析
(1)证明:因为PD⊥平面ABCD,BC
由∠BCD=900,得CD⊥BC,
又PD

所以BC⊥平面PCD。
因为PC
(2)
(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=

(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得

由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积
因为PD⊥平面ABCD,DC
又PD=DC=1,所以
由PC⊥BC,BC=1,得

由


故点A到平面PBC的距离等于
知识点
如图,在四棱锥
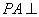
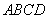
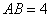
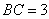
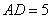
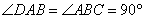
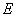
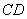
(1)证明: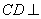

(2)若直线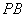

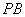
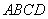
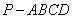
正确答案
见解析
解析
解法1:(1)如图(1),连接AC,由AB=4,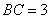
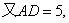
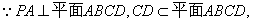
而
(2)过点B作
由(1)CD⊥平面PAE知,BG⊥平面PAE.于是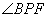
所成的角,且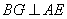
由
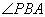
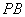
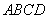
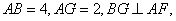
因为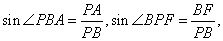
由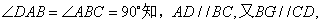
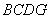

在
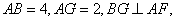
于是
又梯形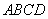
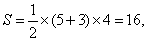
解法2:如图(2),以A为坐标原点,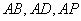
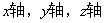
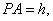
(1)易知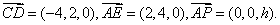

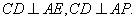
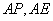
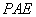
(2)由题设和(1)知,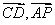
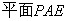
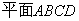
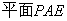
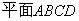
由(1)知,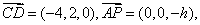

解得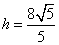
又梯形ABCD的面积为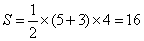
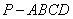
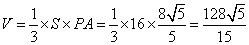
知识点
扫码查看完整答案与解析