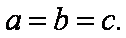- 任意角的概念
- 共691题
在
A
B
C
D
正确答案
解析
由正弦定理
知识点
若等边
A
B
C
D
正确答案
解析
∵等边
∴
∴
故选D.
知识点
衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰。若现有500人参加测试，学生成绩的频率分布直方图如下：
（1）求获得参赛资格的人数；
（2）根据频率直方图，估算这500名学生测试的平均成绩；
（3）若知识竞赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为
正确答案
见解析
解析
解析：（1）获得参赛资格的人数
（2）平均成绩：
（3）设甲答对每一道题的概率为.P
则
知识点
在△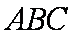
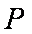
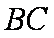
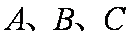
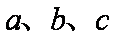
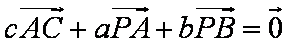
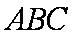
正确答案
解析
由题意知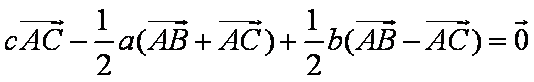
∴
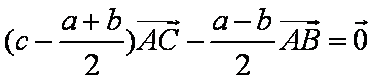
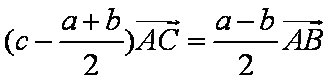
又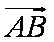
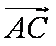
知识点
如图,在三棱锥
（1）求证:
（2）当
正确答案
见解析
解析
解析:（1）证明: 
又
又已知
（2）解法一:如图,以
由于
可设
设平面
则
可得
由（1）可知
易求
二面角
知识点
扫码查看完整答案与解析