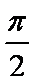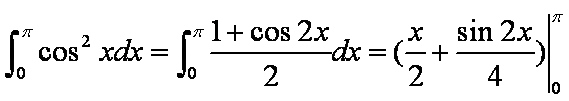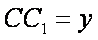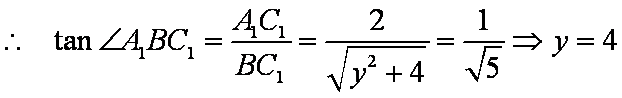- 任意角的概念
- 共691题
如图所示,PA为
(1)求证:
(2)求AC的值.
正确答案
见解析
解析
(1)∵


又



(2)∵



∴
又∵



由(1)知,


∴

∴AC=
知识点
计算: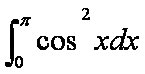
正确答案
解析
由定积分的定义得

知识点
已知椭圆


(1)求椭圆
(2)直线




正确答案
(1)
解析
解析:(1)解法1:由抛物线方程,得焦点

故
又椭圆


由①②消去



从而

解法2:由抛物线方程,得焦点
故椭圆的方程为
(2)

所以,

由
显然





由抛物线的定义,得
综上,当直线l垂直于


知识点
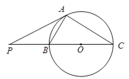
如图,PA是圆O的切线,切点为A,PO交圆O于B,C两点,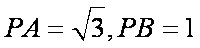
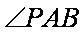
正确答案
30○
解析
因为PA是圆O的切线,由切割线定理得,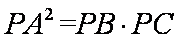
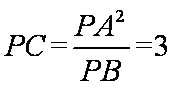
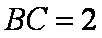
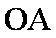
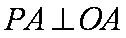
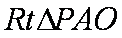
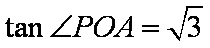
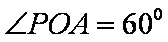
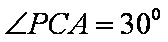
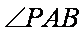
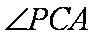
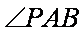
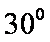
知识点
在如图所示的几何体中,







(1)证明:

(2)求二面角
正确答案
见解析。
解析
(1)因为




故以
则相关各点的坐标分别是





所以
因为平面

所以
又因为



(2)由(1)知,


设





设





设二面角




知识点
在直角坐标系x Oy中,直线 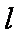
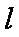
正确答案
解析
由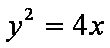
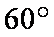
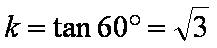
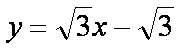
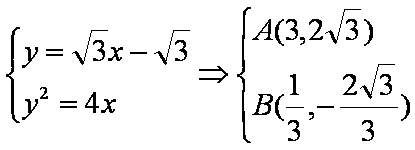
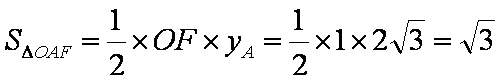
知识点
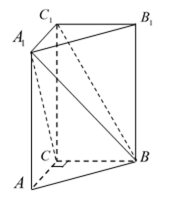
如图,在直三棱柱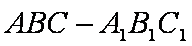
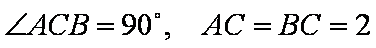
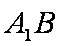
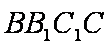
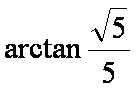
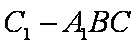
正确答案
见解析
解析
法一: 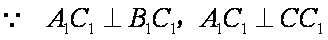
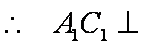
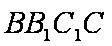
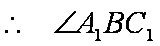
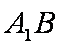
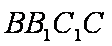
设
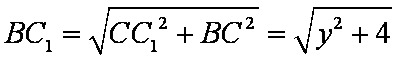
所以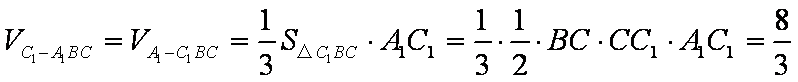
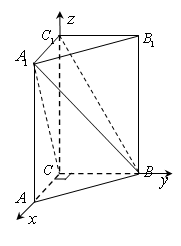
法二:如图,建立空间直角坐标系,设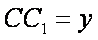
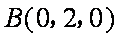
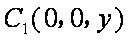
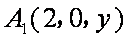
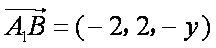
平面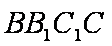
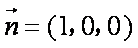
设直线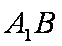
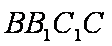
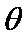
则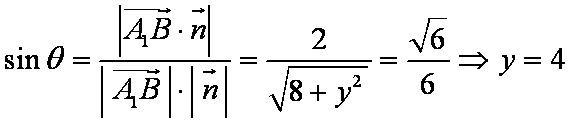
所以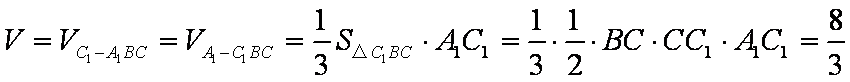
知识点
已知







正确答案
解析
(









(









∴







而cos∠A=

知识点
设



(1)求
(2)求


正确答案
见解析
解析
解析:(1)由

(2)设


此时

知识点
在三角形ABC中,若角A、B、C所对的三边a、b、c成等差数列,则下列结论中正确的是____________。
①b2≥ac;
②
③
④
正确答案
①③④
解析
由a、b、c成等差数列,则
∴
∴
由正弦定理得:
又由余弦定理得:



∴
知识点
扫码查看完整答案与解析