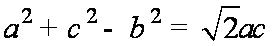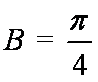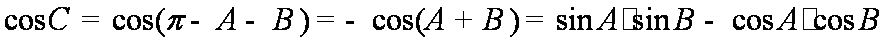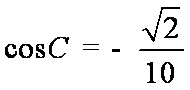- 任意角的概念
- 共691题
16.已知如图,四边形ABCD是直角梯形,AD//BC,CD⊥AD,PA⊥平面ABCD,
(1)求证:BD//平面AEF;
(2)求直线CE与平面PAB所成角的正切值;
(3)求平面AEF与平面ABCD所成二面角的余弦值。
正确答案
见解析。
解析
(1)证明:连接BD,因为E、F分别是PB、PD的中点.在

(2)因为ABCD是直角梯形,CD⊥AD,





故
(3)分别取AB、AD的中点H、G,连接EH、HG、FG,由(Ⅱ)可知,








知识点
15.已知A、B、C是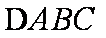
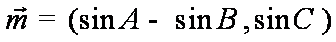
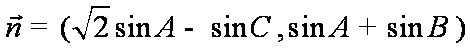
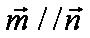
(1)求角B的大小;
(2)若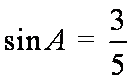
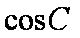
正确答案
见解析。
解析
(1)∵向量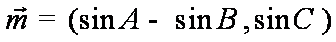
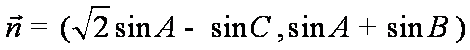
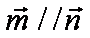
所以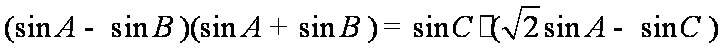
由正弦定理可得: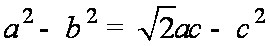
再由余弦定理可得: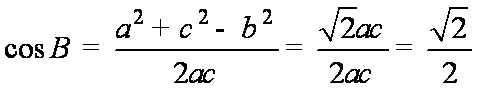
(2)由(1)得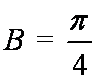
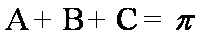
所以
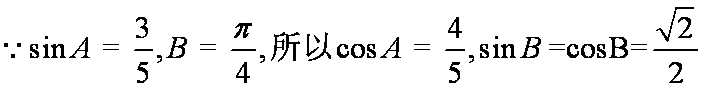
知识点
如图,





(1)若



(2) 求平面

正确答案
见解析。
解析
(1)证明:连结






∴
因为




(2)设平面





则
设平面

则可设
设面

即:

∴
所以平面


知识点
6.已知
正确答案
解析
由于所求的是展开式中所以项的系数和,所以令x=1即可.当x=1时,

知识点
1.已知复数

正确答案
解析

知识点
扫码查看完整答案与解析