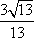- 任意角的概念
- 共691题
在直角三角形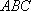
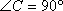
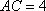
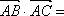
正确答案
16
解析
略
知识点
设





正确答案
解析
略
知识点
已知




(1)求角

正确答案
见解析。
解析
知识点
若△


正确答案
解析
略
知识点
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的参数方程为
正确答案
(2,5)
解析
解:由曲线C1的参数方程为
曲线C2的极坐标方程为ρsinθ﹣ρcosθ=3的直角坐标方程为:y﹣x=3;
解方程组 


故曲线C1与C2的交点坐标为(2,5),
故答案为:(2,5)。
知识点
在



正确答案
解析
略
知识点
函数y=lnx在点A(1,0)处的切线方程为 。
正确答案
y=x﹣1
解析
解:∵y=lnx,∴y′=
∴函数y=lnx在x=1处的切线斜率为1
又∵切点坐标为(1,0)
切线方程为y=x﹣1。
故答案为:y=x﹣1。
知识点
△ABC中内角A,B,C的对边分别为a,b,c,向量


(1)求角A的大小;
(2)若

正确答案
见解析。
解析
解:(1)∵
∴
∴
∴
∴
(2)∵
∴bc=6
由余弦定理得:
⇒(b+c)2=7+3bc=25
∴b+c=5
知识点
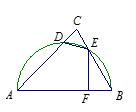
如图,以
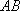
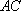
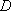
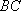
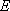
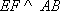
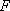
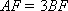
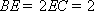

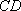
正确答案
60° ;
解析
略
知识点
已知△ABC的内角A,B,C的对边分别为a,b,c,满
(1)求角C
(2)若向量

正确答案
见解析。
解析
(1)∵
∴

∴
∵C∈(0,π),∴
∴

(2)∵向量

由正弦定理得
由余弦定理得c2=a2+b2﹣2absinC,
∴
联立

知识点
扫码查看完整答案与解析