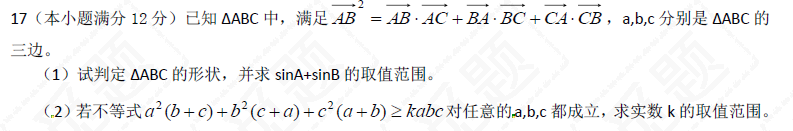热门试卷

（1）证明：∵D，C，E，F分别是AQ，BQ，AP，BP的中点，

∴EF∥AB，DC∥AB，

∴EF∥DC

又EF⊄平面PCD，DC⊂平面PCD，

∴EF∥平面PCD

又EF⊂平面EFQ，平面EFQ∩平面PCD=GH，

∴EF∥GH

又EF∥AB，

∴AB∥GH

（2）解：在△ABQ中，∵AQ=2BD，AD=DQ，∴∠ABQ=90°，即AB⊥BQ。

又PB⊥平面ABQ，∴BA，BQ，BP两两垂直。

以B为坐标原点，分别以BA，BQ，BP所在直线为x轴，y轴，z轴，

建立如图所示的空间直角坐标系。设BA=BQ=BP=2，

则B（0，0，0），Q（0，2，0），D（1，1，0），

C（0，1，0），P（0，0，2），

∴=（﹣1，﹣1，2），=（0，﹣1，2）

设平面PCD的一个法向量为=（x，y，z），

由•=0，•=0，得

，取z=1，得=（0，2，1）

又=（0，2，0）为平面PAB的一个法向量，

∴cos＜n，＞==

设平面PAB与平面PCD所成角为θ，

则sinθ==．

故平面PAB与平面PCD所成角的正弦值为