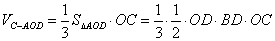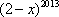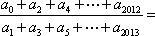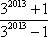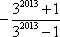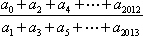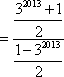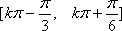- 任意角的概念
- 共691题
如图,









(1)当点

(2)若

正确答案
见解析。
解析
(1)把


∴点坐
由 

∴过点

直线

∴直线

(2)设
∵ 过点

∴ 直线

直线


设


因为

半径为
且
所以
联立①②消去


所以



所以
∵

所以过点
知识点
如图,平行四边形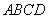
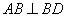
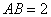
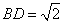
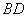
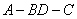

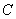

(1)当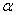
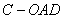
(2)当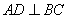

正确答案
见解析。
解析
(1)由题知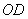
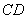
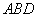
∵
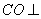
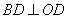
∴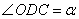
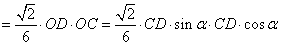
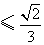
当且仅当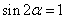
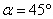
∴当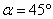
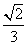
(2)(法一)
连接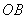
∵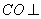
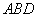
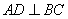
∴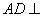
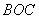
∴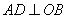
∴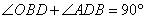
故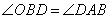
∴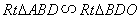
∴
∴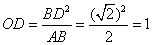
在
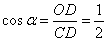
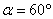
(法二)
过
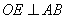
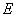
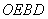
以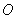
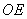
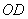
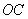
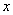
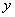
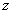
则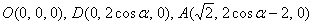
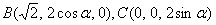
于是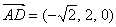
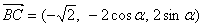
由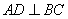
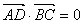
∴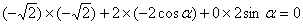
得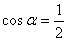
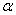
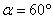
知识点
已知△ABC的三个内角A、B、C所对的边分别为


(1)求cosC的值;
(2)当

正确答案
见解析。
解析
(1)在△ABC中,因为

又

所以


所以
(2)由(1)知
所以

又

知识点
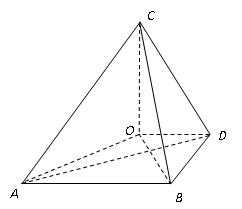
如图,在三棱锥A-BCD中,△ABD和△BCD是两个全等的等腰直角三角形,O为BD的中点,且AB=AD=CB=CD=2,AC=
(1)当
(2)当二面角


正确答案
见解析 。
解析
(1)根据题意知,在△AOC中,

所以
因为AO是等腰直角E角形ABD的中线,所以AO⊥BD。
又BD
(2)
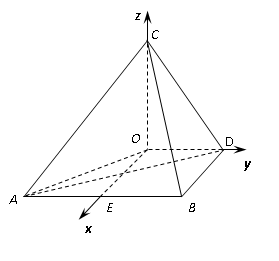
法一 由题易知,CO⊥OD,如图,以O为原点,
OC、OD所在的直线分别为


则有O(0,0,0),


设


设平面ABD的法向量为
则
所以


所以
因为平面BCD的一个法向量为
且二面角


即

因为

解得


设平面ABC的法向量为
因为

则
令



设二面角


所以


法二 在△ABD中,BD⊥AO,在△BCD中,BD⊥CO,
所以∠AOC是二面角

如图,过点A作CO的垂线交CO的延长线于点H,
因为BD⊥CO,BD⊥AO,且CO
所以BD⊥平面AOC。
因为AH
又CO⊥AH,且CO
过点A作AK⊥BC,垂足为K,连接HK。
因为BC⊥AH,AK
因为HK
所以∠AKH为二面角
在△AOH中,∠AOH=



所以
在Rt△CHK中,∠HCK=

在Rt△AHK中,
所以二面角

知识点
若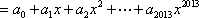
正确答案
解析
令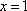
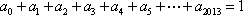
令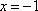
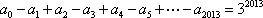
由①②联立,可得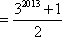
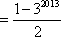
从而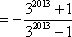
知识点
在△ABC中,三个内角分别为A,B,C,已知

(1)求cosC的值;
(2)若BC=10,D为AB的中点,求CD的长。
正确答案
见解析。
解析
(1)因为


则

(2)由(1)可得
由正弦定理得

因为在△BCD中,

所以
知识点
已知函数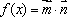
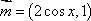
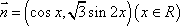
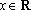
(1)求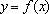
(2)在△

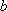

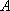
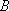
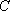
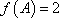
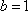
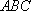
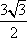

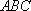
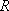
正确答案
见解析
解析
(1)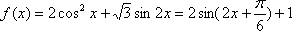
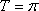
单调递增区间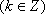
(2)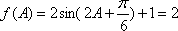
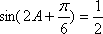
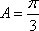
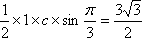
∴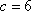
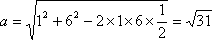
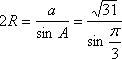
∴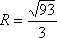
知识点
在平面直角坐标系




(1)求
(2) 求
正确答案
见解析。
解析
本小题考查三角函数的定义、两角和的正切、二倍角的正切公式。
(1)由条件得 





因此

(2)




且

同理

从而
知识点
已知椭圆





(1)求椭圆
(2)设经过点





(3)是否存在直线





正确答案
见解析
解析
(1)由△


故椭圆方程为
(2)设直线



则有
由韦达定理得
点


因为
设


由

…………10分
(3)假设存在直线




设
因为


于是设直线

由

由



由题意应有

故
得
即
整理得
解得

经检验,当


当



知识点
已知向量


(1)求函数
(2)已知





正确答案
见解析
解析
(1)由条件得



(2)由






知识点
扫码查看完整答案与解析