- 直线与椭圆的位置关系
- 共19题
在极坐标系中,过点

正确答案
解析
略
知识点
已知椭圆







(1)求椭圆
(2)证明直线

正确答案
见解析
解析
(1)由题意知:
所以,焦点坐标为

(2)由题意知:直线PB的斜率存在,设直线PB的方程为



由
则
直线AE的方程为


又


把(1)代入(3)式,整理得


知识点
已知椭圆














(1) 求椭圆
(2) 是否存在满足



正确答案
见解析。
解析
(1) 解法1:设椭圆

依题意: 
∴ 椭圆

解法2:设椭圆

根据椭圆的定义得

∵

∴ 椭圆

(2)解法1:设点



∵
∴
∴
化简得:
由


∴抛物线



即
同理,抛物线



设点

而

代入②得 
则




若




∵直线


∴直线

∴满足条件

解法2:设点


由


∴抛物线



即
∵

∵点


同理, 
综合①、②得,点

∵经过
∴直线

∵点


∴点

若



∵直线


∴直线

∴满足条件

解法3:显然直线


由


设

由


∴抛物线



即
∵

同理,得抛物线



由
∴
∵
∴点

∴
化简得
由
可得方程(*)有两个不等的实数根. ∴满足条件的点
知识点
已知数列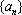
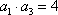
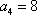
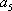
正确答案
-16或 16
解析
略
知识点
济南市“两会”召开前,某政协委员针对自己提出的“环保提案”对某处的环境状况进行了实地调研.据测定,该处的污染指数与附近污染源的强度成正比,与到污染源的距离成反比,比例常数为k(k>0)。现已知相距36 km的A,B两家化工厂(污染源)的污染强度分别为正数a,b,它们连线上任意一点C处的污染指数y等于两化工厂对该处的污染指数之和.设AC=x(km)。
(1) 试将y表示为x的函数;
(2) 若a=1时,y在x=6处取得最小值,试求b的值.
正确答案
见解析。
解析
(1) 设点C受A污染源污染指数为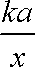
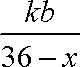
从而点C处污染指数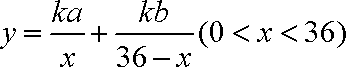
(2) 因为a=1,所以,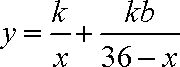
y′=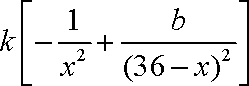
令y′=0,得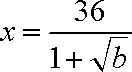
当x∈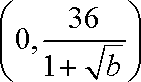
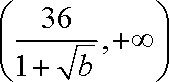
∴当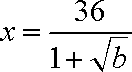
又此时x=6,解得b=25,经验证符合题意.
所以,污染源B的污染强度b的值为25…………………………………12分
知识点
扫码查看完整答案与解析















