集合的概念及运算
共879题

集合的概念及运算
共879题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

函数的图象大致是

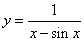
正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

是虚数单位，若，则等于（）

正确答案

解析

知识点

集合的含义

题型：简答题

简答题 · 18 分

过坐标原点作倾斜角为的直线交抛物线于点，过点作倾斜角为的直线交轴于点，交于点；过点作倾斜角为的直线交轴于点，交于点；过点作倾斜角为的直线，交轴于点，交于点；如此下去……，又设线段的长分别为，数列的前项的和为。

（1）求；

（2）求，；

（3）设，数列的前项和为，若正整数成等差数列，且，试比较与的大小。

正确答案

（1）,（2）,（3）

解析

（1）如图，由是边长为的等边三角形，得点的坐标为，又在抛物线上，所以，得

同理在抛物线上，得

（2）如图，法1：点的坐标为，即点，所以直线的方程为或，因此，点的坐标满足

消去得，所以

又，故

从而 ……①

由①有 ……②

②-①得

即，又，于是

所以是以为首项、为公差的等差数，

（3）因为，

所以数列是正项等比数列，且公比，首项，

因正整数成等差数列，且，设其公差为，则

为正整数，所以，，

则，，，… 2分

而

因为，所以，

又为正整数，所以与同号，

故，所以，。

知识点

集合的含义

题型：简答题

简答题 · 14 分

已知双曲线：的中心为原点，左，右焦点分别为，，离心率为，点是直线上任意一点，点在双曲线上，且满足。

（1）求实数的值；

（2）证明：直线与直线的斜率之积是定值；

（3）若点的纵坐标为，过点作动直线与双曲线右支交于不同两点，，在线段上取异于点，的点，满足，证明点恒在一条定直线上。

正确答案

见解析。

解析

（1）解：设双曲线的半焦距为，

由题意可得

解得，

（2）证明：由（1）可知，直线，点，设点,，

因为，所以。

所以。

因为点在双曲线上，所以，即。

所以

。

所以直线与直线的斜率之积是定值。

（3）证法1：设点，且过点的直线与双曲线的右支交于不同两点，，由（2）知，。

设，则。

即

整理，得

由①×③，②×④得

将，代入⑥，得。 ⑦

将⑤代入⑦，得。

所以点恒在定直线上。

证法2：依题意，直线的斜率存在。

设直线的方程为，

由

消去得。

因为直线与双曲线的右支交于不同两点，，

则有

设点，由，得。

整理得。

将②③代入上式得。

整理得。 ④

因为点在直线上，所以， ⑤

联立④⑤消去得。

所以点恒在定直线上。

知识点

集合的含义

题型：简答题

简答题 · 14 分

已知椭圆的中心在坐标原点，焦点在坐标轴上，且经过两点。

（1）求椭圆的方程；

（2）若平行于的直线在轴上的截距为，直线交椭圆于两个不同点，直线与的斜率分别为，求证：。

正确答案

见解析

解析

（1）设椭圆的方程为

将代入椭圆的方程，得

解得，所以椭圆的方程为

设点的坐标为，则。

又是上的动点，所以，得，代入上式得

，

故时，。的最大值为。

（2）因为直线平行于，且在轴上的截距为，又，所以直线的方程为，由得

设、，则。

又

故。

又，

所以上式分子

故。

所以直线与直线的倾斜角互补。

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知命题，命题，则p是q的

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

曲线上的点到直线的距离的最小值为

正确答案

解析

略

知识点

集合的含义

题型：填空题

填空题 · 5 分

对于函数，若存在区间，则称函数为“同域函数”，区间A为函数的一个“同城区间”.给出下列四个函数：

①；②；③；④log.

存在“同域区间”的“同域函数”的序号是_______________（请写出所有正确的序号）

正确答案

①②③

解析

略

知识点

集合的含义

题型：单选题

单选题 · 5 分

已知是实数，是纯虚数，则等于（）

正确答案

解析

是纯虚数，则；，选A

知识点

集合的含义

题型：单选题

单选题 · 5 分

在区间之间随机抽取一个数,则满足的概率为( )

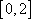
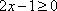
正确答案

解析

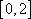
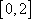
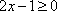
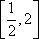
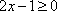
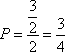
区间看作总长度为2，区间中满足的只是，长度为，因为是随机抽取的一个数，由几何概型计算公式知满足的概率为.答案：

知识点

集合的含义

继续学习学习下一知识点

下一知识点 : 命题及其关系、充分条件与必要条件

百度题库 > 高考 > 文科数学 > 集合的概念及运算

扫码查看完整答案与解析