- 集合的概念及运算
- 共879题
某中学共有学生2000人,各年级男,女生人数如下表:
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19。
(1)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(2)已知y≥245,z≥245,求高三年级中女生比男生多的概率。
正确答案
见解析。
解析
(1)∵
高三年级人数为y+z=2000﹣(373+377+380+370)=500
现用分层抽样的方法在全校抽取48名学生,
应在高三年级抽取的人数为
(2)设高三年级女生比男生多的事件为A,高三年级女生,男生数记为(y,z),由(2)知y+z=500,且y,z∈N,基本事件空间包含的基本事件有(245,255),(246,254),(247,253),┅,(255,245)共11个。事件A包含的基本事件(251,249),(252,248),(253,247),(254,246),(255,245)共5个。
∴
知识点
若集合A={


正确答案
解析



知识点
设集合A= {-1,0,2),集合
正确答案
解析
解析:当











故选:A
知识点
设集合A={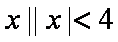
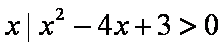
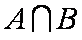
正确答案
解析
试题分析:因为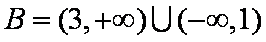
知识点
已知集合


正确答案
2
解析



知识点
设全集U=R,集合A={x|x≥2},B={x|0≤x<5},则集合(∁UA)∩B=( )
正确答案
解析
∵全集U=R,集合A={x|x≥2}
∴CUA={x|x<2}
∵B={x|0≤x<5}
∴(CUA)∩B={x|0≤x<2}
知识点
已知集合A={x||2x﹣1|≤3},B=(﹣3,a),若A∩B=A,则实数a的取值集合是 。
正确答案
(2,+∞)
解析
∵|2x﹣1|≤3
∴﹣3≤2x﹣1≤3
∴﹣2≤2x≤4
∴﹣1≤x≤2
故A=[﹣1,2]
又∵B=(﹣3,a),
若A∩B=A
则a>2
故实数a的取值集合是(2,+∞)
知识点







正确答案
见解析。
解析


∴
由已知:
∴
知识点
集合A={x||x﹣2|≤2},B={y|y=﹣x2,﹣1≤x≤2},则A∩B=( )
正确答案
解析
∵|x﹣2|≤2,
∴﹣2≤x﹣2≤2,
∴0≤x≤4,即A={x|0≤x≤4};
又B={y|y=﹣x2,﹣1≤x≤2}={y|﹣4≤y≤0},
∴A∩B={0}。
知识点
已知集合
正确答案
解析
知识点
扫码查看完整答案与解析