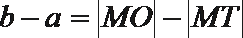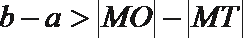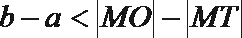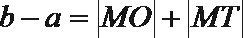- 双曲线的几何性质
- 共199题
15.已知点
正确答案
解析
根据题意作图
容易得到
由双曲线的几何性质
考查方向
解题思路
【解题思路】本题属于基础题型，使用数形结合，
易错点
该题不易发现使用几何性质，导致运算变大，运算出错
知识点
10.双曲线
A
B2
C
D
正确答案
解析
圆心坐标为
考查方向
本题主要考查了离心率的求解/本题主要考查运算求解能力
易错点
找不到关于ａ、ｂ、ｃ的方程，计算量大，容易出现计算错误。
知识点
7． 若椭圆
A3
B
C21
D84
正确答案
解析
由椭圆和双曲线的定义，得
考查方向
本题主要考查了椭圆和双曲线的定义。
易错点
本题易在利用双曲线定义得到
知识点
3．若实数数列：
A
B
C
D
正确答案
解析
由
考查方向
本题主要考查等比数列的概念和椭圆的离心率的概念。
解题思路
由等比数列求出a,代入圆锥曲线方程求出离心率。
易错点
1、等比数列概念不清导致a 漏负解
2、误认为圆锥曲线只是椭圆导致漏解。
知识点
11．过双曲线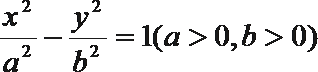
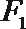
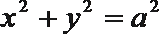
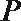
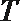
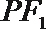
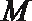
A
B
C
D
正确答案
解析
连结P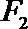
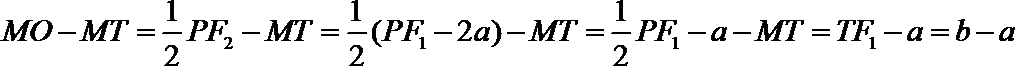
考查方向
本题考查学生的解析几何的综合运用的能力。
解题思路
将已知线段向焦半径转化，利用双曲线的性质解决。
易错点
1、不能正确地将已知条件进行转化；
2、解决综合问题的能力不强。
知识点
3.已知双曲线c: 
Ay=
By=
Cy=
Dy=±x
正确答案
解析
先根据离心率求出双曲线a和b的关系式，利用双曲线中a2+b2=c2 的恒等式，求得渐近线的方程，所以选C
考查方向
本题主要考查双曲线的离心率和渐近线方程，考查学生的基本知识掌握能力
解题思路
利用离心率求渐进线方程。
易错点
记混双曲线离心率以及渐近线方程的求法。
知识点
10．过双曲线
A
B
C
D
正确答案
解析
由题可知，1<b/a<3, 则e2=1+b2/a2∈(2,10),则e∈
考查方向
本题主要考查直线与双曲线的位置关系
解题思路
（1）表示直线方程；（2）利用双曲线的几何性质表示离心率e，即可得到结果。
A选项不正确，B选项不正确，D选项不正确，所以选C选项。
易错点
本题易在表示直线方程时发生错误。
知识点
10． 已知双曲线
正确答案
2，
解析
双曲线
考查方向
本题考查了双曲线的渐近线、离心率，在近几年的各省高考题出现的频率较高．
解题思路
通过渐近线先求出b的值，再求出离心率．
易错点
注意双曲线中是
知识点
13．已知双曲线
正确答案
解析
本题考查抛物线的焦点坐标，双曲线的离心率、焦点坐标、渐近线方程等知识。
解：因为抛物线为
考查方向
本题主要考查了抛物线的焦点坐标，双曲线的离心率、焦点坐标、渐近线方程等知识，在各地的高考题中出现的频率较高，属于中档题，考查学生对基础知识的掌握与分析问题的能力。
易错点
双曲线中c2=a2+b2,易与椭圆中a2=b2+c2 搞混．
知识点
7.已知双曲线
A
B
C
D
正确答案
解析
易知，抛物线焦点坐标为
考查方向
本题主要考查了求双曲线的标准方程，在近几年的各省高考题出现的频率较高，常与椭圆、抛物线等知识点交汇命题。
解题思路
先求出抛物线的焦点坐标，即求出此b，再根据c2=a2+b2即可求出双曲线的标准方程。
易错点
抛物线与双曲线定义不清楚导致出错。
知识点
扫码查看完整答案与解析