• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 双曲线的几何性质
  • 共199题
  • 双曲线的几何性质
  • 共199题

热门试卷

X 查看更多试卷
1
题型：填空题
|
填空题 · 5 分

已知双曲线（a＞0，b＞0）的一条渐近线为2x+y=0，一个焦点为（ ,0），则a=_______；b=_____________.

正确答案

a=1， b=2

知识点

双曲线的几何性质
1
题型： 单选题
|
单选题 · 5 分

4.已知双曲线的焦距为，且双曲线的一条渐近线与直线垂直，则双曲线的方程为

A

B

C

D

正确答案

A

知识点

双曲线的几何性质
1
题型：填空题
|
填空题 · 5 分

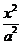
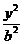
14.已知双曲线E：–=1（a>0，b>0）．矩形ABCD的四个顶点在E上，AB，CD的中点为E的两个焦点，且2|AB|=3|BC|，则E的离心率是_______．

正确答案

2

知识点

双曲线的定义及标准方程双曲线的几何性质
1
题型：填空题
|
填空题 · 5 分

3.在平面直角坐标系xOy中，双曲线的焦距是_______________.

正确答案

知识点

双曲线的定义及标准方程双曲线的几何性质
1
题型：简答题
|
简答题 · 14 分

21.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分.

双曲线的左、右焦点分别为F1、F2，直线l过F2且与双曲线交于A、B两点.

（1）若l的倾斜角为 ，是等边三角形，求双曲线的渐近线方程；

（2）设 若l的斜率存在，且|AB|=4，求l的斜率.

正确答案

（1）设．

由题意，，，，

因为是等边三角形，所以，

即，解得．

故双曲线的渐近线方程为．

（2）由已知，．

设，，直线．

由，得．

因为与双曲线交于两点，所以，且．

由，，得，

故，

解得，故的斜率为．

知识点

双曲线的几何性质
1
题型：填空题
|
填空题 · 5 分

14.已知双曲线E：–=1（a>0，b>0）．矩形ABCD的四个顶点在E上，AB，CD的中点为E的两个焦点，且2|AB|=3|BC|，则E的离心率是_______．

正确答案

2

解析

由已知易得，，所以，，由，得离心率或（舍去），所以离心率为2.

考查方向

双曲线的性质，离心率的求法，推理分析与计算求解能力，难度中等。

解题思路

根据双曲线的性质设出A、B点的坐标涉及到的两个线段的长度表示出来，结合题给等量关系求解。

易错点

注意双曲线离心率的取值范围e>1。

知识点

双曲线的几何性质
1
题型：填空题
|
填空题 · 5 分

10．已知双曲线 的一条渐近线过点 ，且双曲线的一个焦点在抛物线 的准线上，则双曲线的方程为___________

正确答案

解析

将代入渐近线方程，得a=2b. c=,c2=a2+b2, a2+.

考查方向

本题主要考查了双曲线的方程及双曲线与抛物线的基本知识。

解题思路

本题考查运用双曲线的渐近线方程及抛物线的准线方程，求a,b，解题步骤如下：将代入渐近线方程，得a=2b. 由双曲线的一个焦点在抛物线 的准线上，可知c=,c2=a2+b2, a2+.

易错点

本题必须注意审题，忽视则会出现错误。

知识点

双曲线的定义及标准方程双曲线的几何性质抛物线的标准方程和几何性质
1
题型： 单选题
|
单选题 · 5 分

2．若双曲线的焦点在x轴上，则实数k的取值范围是（   ）

A（一∞，1）

B(2，+∞)

C(1,2)

D(一∞,1)U(2,+∞)

正确答案

A

解析

试题分析：本题属于双曲线中的基本问题，题目的难度是简单。

考查方向

本题主要考查了双曲线的标准方程,在近几年的各省高考题出现的频率较高。

解题思路

本题考查双曲线的焦点位置，解题步骤如下：

（1）由题可知，易得x2的系数为正，y2系数为负。

（2）令2-k>0,k-1<0，解得k<1.

易错点

本题易在求解时把分母平方运算。

知识点

双曲线的几何性质
1
题型： 单选题
|
单选题 · 5 分

11．在等腰梯形中，，其中，以为焦点且过点的双曲线的离心率为，以为焦点且过点的椭圆的离心率为，若对任意都有不等式恒成立，则的最大值为（    ）

A

B

C

D

正确答案

C

解析

在等腰梯形ABCD中，

BD2=AD2+AB2-2AD•AB•cos∠DAB=1+4-2×1×2×（1-x）=1+4x，

由双曲线的定义可得a1=，，

由椭圆的定义可得，

则

令

则在上单调递减，

∴

考查方向

本题主要考查了圆锥曲线的定义、性质与方程

解题思路

先利用双曲线和椭圆的性质，求出，利用函数单调性求出其最小值即可

易错点

（1）利用根据余弦定理表示出BD，进而根据双曲线的定义可得到a1的值

（2）利用换元法即可求出e1+e2的取值范围

知识点

不等式恒成立问题双曲线的几何性质
1
题型： 单选题
|
单选题 · 5 分

A

B

C

D

正确答案

D

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题
继续学习 学习下一知识点
下一知识点 : 双曲线的相关应用
百度题库 > 高考 > 文科数学 > 双曲线的几何性质

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题