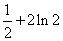- 微积分基本定理
- 共11题
已知函数






正确答案
解析
由
知识点


正确答案
-120
解析
略
知识点
f(x)对任意x∈R都有
(1)求

(2)数列{an}满足:an=f(0)+
(3)令
正确答案
见解析。
解析
(1)因为
令x=


(2)an=f(0)+
又an=f(1)+f(

两式相加 2an=[f(0)+f(1)]+[f(
所以an=
又
(3)
=
=
知识点

正确答案
解析
知识点
某个部件由三个元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布
正确答案
解析
三个电子元件的使用寿命均服从正态分布
得:三个电子元件的使用寿命超过1000小时的概率为
超过1000小时时元件1或元件2正常工作的概率
那么该部件的使用寿命超过1000小时的概率为
知识点
曲线

正确答案

解析
略
知识点
己知函数

(1)求
(2)在△ABC中,a、b、c分别是A、B、C的对边,已知a=l,b=

正确答案
见解析
解析
(1)
=

因为





(2)由(1)知






当



综上,
知识点
12.函数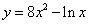
正确答案
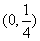
解析
解析已在路上飞奔,马上就到!
知识点
6.x=
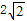
正确答案
解析
∵ x=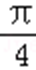
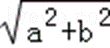
其中,cosθ=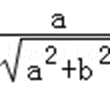
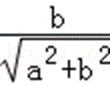
且函数f(x)的最大值为2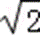
则a2+b2=8,f(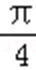


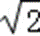


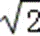
可得a+b=4,或a+b=﹣4,
∴a=b=2,或 a=b=﹣2,g(x)=2sinx+2,或g(x)=﹣2sinx﹣2,
故g(x)=asinx+b的最大值可能为0,故选:B.
知识点
5.已知某随机变量X的概率密度函数为P(x)=
正确答案
解析
知识点
扫码查看完整答案与解析