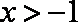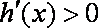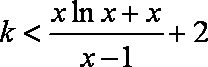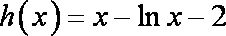- 一元高次不等式的解法
- 共47题
已知函数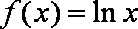

(1)设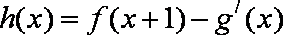
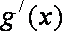
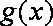
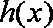

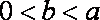
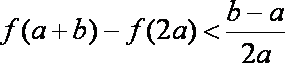
(3)设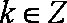
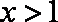

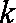
正确答案
见解析
解析
(1)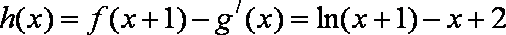
所以 
当

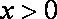
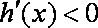
因此,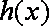
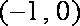
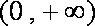
因此,当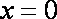
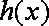
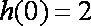
(2)当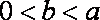
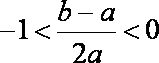
由(1)知:当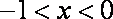
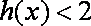
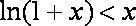
因此,有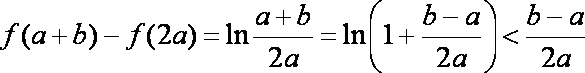
(3)不等式
所以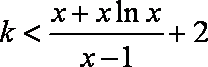
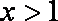
令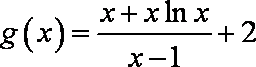
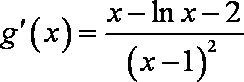
令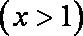
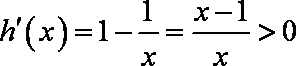
所以函数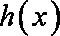
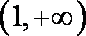
因为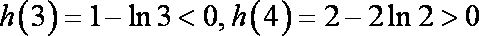
所以方程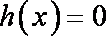
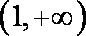
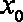
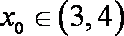
当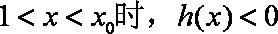
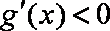
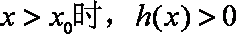
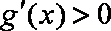
所以函数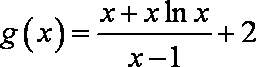
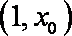
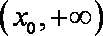
所以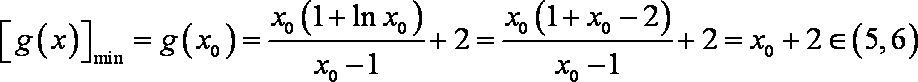
所以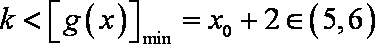
故整数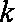
知识点
函数
正确答案
解析
知识点
已知各项均为正数的数列{




(1)求数列{

(2)若


正确答案
(1)
解析
(1)∵
∴
∵数列{

∴
即


∵

∴


∴数列{

(2)由(1)及


∵
∴
∴
②-1得,
=
要使S
∴使S
知识点
由曲线所围成图形的面积是____________.
正确答案
解析
略
知识点
时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量y(单位:千套)与销售价格x(单位:元/套)满足的关系式
(1)求m的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格x的值,使网校每日销售套题所获得的利润最大(保留1位小数)
正确答案
(1)m=10(2)3.3
解析
(1)因为销售价格为4元/套时,每日可售出套题21千套,所以x=4时,y=21,
代入关系式

解得m=10。
(2)由(1)可知,套题每日的销售量
所以每日销售套题所获得的利润
从而f'(x)=12x2﹣112x+240=4(3x﹣10)(x﹣6)(2<x<6)。
令f'(x)=0,得


所以
所以当
故当销售价格为3.3元/套时,网校每日销售套题所获得的利润最大。
知识点
扫码查看完整答案与解析