- 不等式的证明
- 共16题
20.已知函数

(1)求证:
(2)当




正确答案
(1)
依题意

(2)






即
考虑函数



所以



由




解析
解析已在路上飞奔,马上就到!
知识点
请考生在第(22)、(23)两题中任选一题作答。注意:只能做所选定的题目。如果多做,则按所做的第一个题目计分。
22.如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T,(不与a、b重合),DN与圆O相切于点N,连结MC,MB,OT。
(I)求证:
(II) 若

23.已知函数
(I)解不等式 
(II)若


正确答案
22.(1)证明:因MD与圆O相交于点T,由切割线定
理




则

所以
(2)由(1)可知,

故


根据圆周角定理得,
23.(1)由题
因此只须解不等式
当


当


当


综上,原不等式的解集为
(2)由题
当

解析
解析已在路上飞奔,马上就到!
知识点
已知x,y,z均为正数,求证: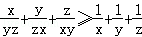
正确答案
见解析。
解析
因为x,y,z都是为正数,
所以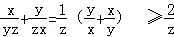
同理可得
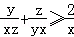
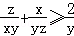
当且仅当x=y=z时,以上三式等号都成立。
将上述三个不等式两边分别相加,并除以2,
得:
知识点
已知

正确答案
见解析
解析
证明:由柯西不等式得
则
知识点
设a、b是非负实数,求证:
正确答案
见解析。
解析
(方法一)证明:
因为实数a、b≥0,
所以上式≥0。即有
(方法二)证明:由a、b是非负实数,作差得
当



当



所以
知识点
将一个正整数






(1)写出
(2)对任意正整数


(3)当正整数

正确答案
见解析
解析
(1)解:因为3=3,3=1+2,3=1+1+1,所以
因
所以
(2)结论是
证明如下:由结论知,只需证
因为









所以





同样,把一个








所以有
(3)由第(2)问可知:
当正整数

又

对于*式,分别取


即
知识点
已知函数
(1)解不等式
(2)若

正确答案
见解析
解析
(1)f(x)+f(x+4)=|x-1|+|x+3|=
当x<-3时,由-2x-2≥8,解得x≤-5;
当-3≤x≤1时,f(x)≤8不成立;
当x>1时,由2x+2≥8,解得x≥3. …4分
所以不等式f(x)≤4的解集为{x|x≤-5,或x≥3}, …5分
(2)f(ab)>|a|f(),即|ab-1|>|a-b|, …6分
因为|a|<1,|b|<1,所以|ab-1|2-|a-b|2
=(a2b2-2ab+1)-(a2-2ab+b2)
=(a2-1)(b2-1)>0,
所以|ab-1|>|a-b|,故所证不等式成立, 10分
知识点
已知x>0, y>0,证明:(1+x+y2)( 1+x2+y)≥9xy.
正确答案
见解析。
解析
因为x>0, y>0, 所以1+x+y2≥

所以(1+x+y2)( 1+x2+y)≥
知识点
20.若由数列




(I)在数列


(II)若数列
(III)若数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数

(1)求a,b的值;
(2)证明:
正确答案
由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴
因此实数a,b的值分别为-1和3.
(2)证明 f(x)=x-x2+3ln x(x>0).
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+

当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在 (0,1)上单调递增;在(1,+∞)上单调递减.
∴g(x)在x=1处有最大值g(1)=0,
∴f(x)-(2x-2)≤0,即f(x)≤2x-2,得证
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析