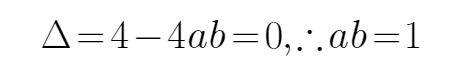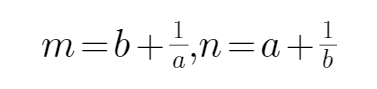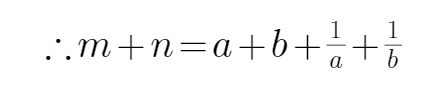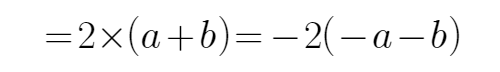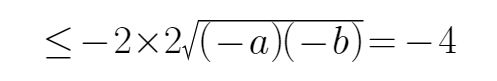基本不等式及不等式的应用
共164题

基本不等式及不等式的应用
共164题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

5．已知，满足约束条件则目标函数的最大值为

正确答案

解析

可行域如图所示：

把目标函数化为直线的斜截式，将其平移经过可行域，找到直线在轴上截距最小时对应的点；将点代入目标函数，求出。

A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查了线性规划问题，除了本题截距型的考查，也要重视斜率型和距离型的题目的考查。

解题思路

可变为，画图可知直线经过某点的时候z最大，即可得到结果。

A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

可行域和目标函数对应的直线的画图出现错误

与截距的关系理解出现偏差

知识点

利用基本不等式求最值

题型：单选题

单选题 · 5 分

6．设为正数，，则 ( )

正确答案

解析

由得.

又

即，所以.

由不等式成立的条件，得，所以

考查方向

本题主要考查基本不等式的知识，意在考查考生的转化能力和化归的能力.

解题思路

1.先根据基本不等式转化题中给出的条件；后得到；2.后根据基本不等式成立的条件即可得到答案。

易错点

1.看不出与之间的内在联系是什么；2.不会变形。

知识点

利用基本不等式求最值平均值不等式

题型：单选题

单选题 · 5 分

若，则的最小值是（）

正确答案

解析

由化同底得：

两边同时除以得：，要使对数有意义知均为正数，由均值不等式：，当且仅当“”时，取“=”号。故选D选项。

考查方向

本题主要考查了对数运算和均值不等式,在近几年的各省高考题出现的频率较高，属于难题。

解题思路

1、由得到的等量关系；2、由均值不等式求出的最小值。

易错点

1、本题易在对数运算上卡住，难以得到的等量关系； 2、对均值不等式的结构不熟悉导致解题出错；

知识点

对数的运算性质利用基本不等式求最值

题型：单选题

单选题 · 5 分

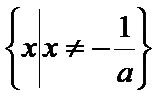
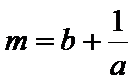
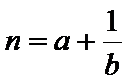
9．已知a，b同号，二次不等式ax2+2x+b＜0的解集为，且,，则m+n的最大值是

C﹣2

D﹣4

正确答案

解析

根据不等式的解集可以判断，方程有两个不等的实数根

所以

又

当且仅当a=b时，可得m+n的最大值为-4，所以选D

考查方向

一元二次不等式的解法

解题思路

根据一元二次不等式的解集得出根的判别式等于0，再利用基本不等式求出m+n的最大值

易错点

不能通过二次不等式的解集判断出方程有两个相等的实数根。

知识点

利用基本不等式求最值

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 基本不等式及不等式的应用

扫码查看完整答案与解析