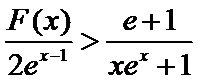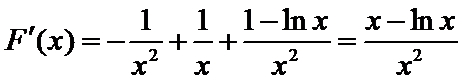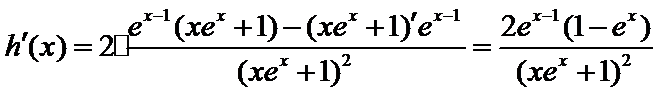- 基本不等式及不等式的应用
- 共164题
已知函数
25.若函数


26.令





27.当
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
正确答案
见解析
解析
考查方向
解题思路
第1问利用导数求函数的单调区间,第2问利用分类讨论思想,讨论参数的值。第3问通过构造函数证明不等式。
易错点
求导数错误,参数的取值范围分类错误
19.已知函数

(1)证明:当|a|≥2时,M(a,b)≥2;
(2)当a
正确答案
(1)详见解析;(2)3;
解析
试题分析:(1)分析题意可知





(1)由f(x)= 














(2)由M(a,b)








考查方向
解题思路
(1)根据a的取值范围,得到函数在[-1,1]上的单调性,分类讨论证得结论;(2)由题中给出的新定义进行求解.
易错点
二次函数在闭区间上的单调性.
知识点
函数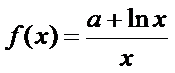
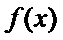

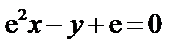
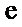

25.若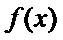
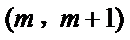


26.求证:当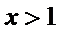
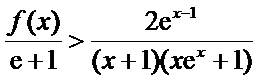
正确答案
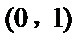
解析
因为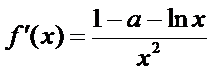
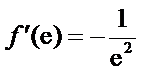
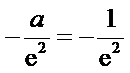
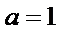
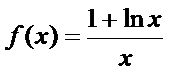
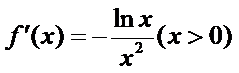
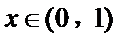
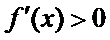
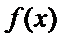
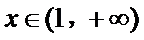
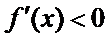
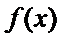
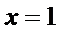
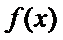
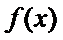
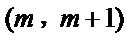
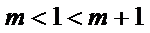
即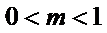
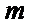
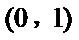
考查方向
解题思路
第一问由切线与直线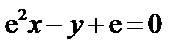
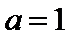
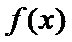
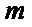
正确答案
略;
解析
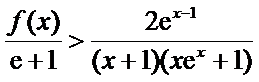
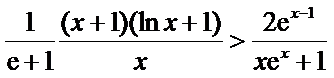
令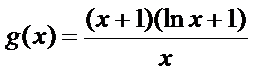
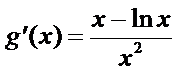
再令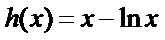
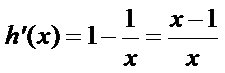
因为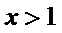
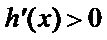
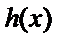
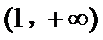
所以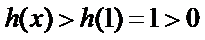
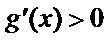
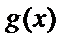
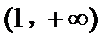
所以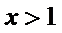
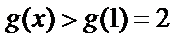

令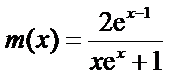

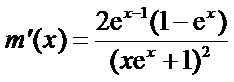
因为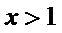
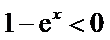
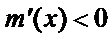
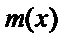
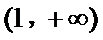
所以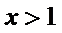
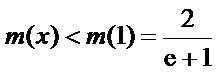
所以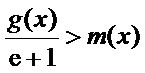
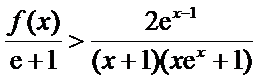
考查方向
解题思路
第二问现将不等式等级变形,构造新函数,对新函数用导函数求最值
已知定义在R上的偶函数


25.当

26.求最大的整数



正确答案
(1)
解析
(1):当


记过原点与

则切线L斜率为
又切线过(0,0),所以



∴当



考查方向
解题思路
先设切点后利用导数的几何意义求出切点坐标后即得切线方程;
易错点
没有给出切点导致无法入手;
正确答案
(2)4
解析
(2)因为任意

当


当


∴ 

又整数


得:

∴ 

令

当


当


又


由此可见,方程


且当






下面证明:

①当




②当

令




∴

综上所述,

考查方向
解题思路
先探求出m的值后证明。
易错点
对于题中给的信息无法处理导致没有思路。
21.已知函数
(I)若函数


(II)证明:
(III)若不等式

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
1)根据共同的切线的理解得到该点处导函数值与函数值都相等得到t
2)利用单调性确定绝对值内的正负,去掉绝对值号,利用
3)构造关于m的一次函数,把x当作参数消掉m后再使用恒成立问题的解答得出结果
易错点
本题易错在以下几个方面
1)对共同的切线理解不足,第一问出错
2)不能有效去掉绝对值,使用错的解题思想
3)变量间关系不能有效理清
知识点
设函数



25.求
26.证明:
正确答案
(1)

解析
试题分析: 本题属于导数的综合应用,考查考生转化与化归数学思想与方法。
(Ⅰ)因为


又点


所以

考查方向
解题思路
(1)利用导数解决曲线的切线问题,从而解出a,b的值
(2)通过构造新函数的方法找到证明不等式的突破口。
易错点
不等式证明如何构造新函数
正确答案
(2)对任意

解析
试题分析: 本题属于导数的综合应用,考查考生转化与化归数学思想与方法。
(Ⅱ)令
因为

所以




我们如果能够证明

下面证明:对任意

由(1)知
则


又



当



当



所以


所以
令
所以

所以
综上,对任意

考查方向
解题思路
(1)利用导数解决曲线的切线问题,从而解出a,b的值
(2)通过构造新函数的方法找到证明不等式的突破口。
易错点
不等式证明如何构造新函数
已知函数f (x)= 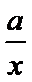
25.若函数f(x)在区间[1,e]上的最小值是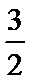
26.当a=1时,设F(x)=f(x)+1+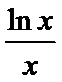
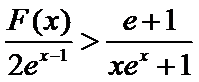
正确答案
(1)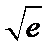
解析
(1)因 为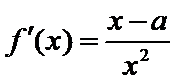
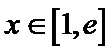
①当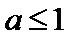
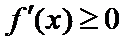
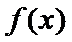
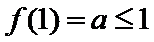
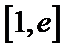
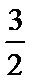
②当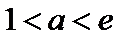
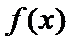
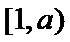
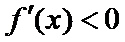
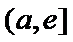
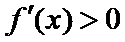
∴函数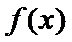
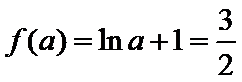
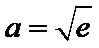
③当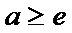
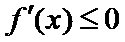
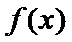
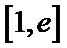
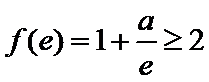
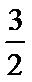
综上所述,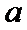
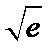
考查方向
解题思路
(1)先对函数进行求导,再对参数进行分类讨论探讨函数的单调性从而研究其最小值及此时a的值 ;(2)通过灵活变形构造新函数的方法证明不等式。
易错点
对参数的分类讨论研究函数的最值。
正确答案
(2)当x>l时,
解析
(2)要证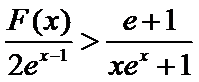
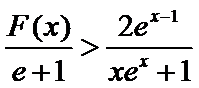
当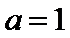
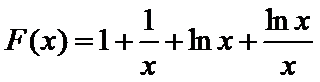
令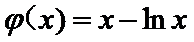
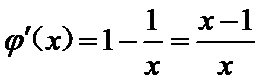
当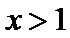
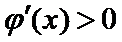
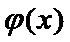
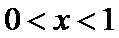
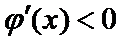
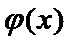
∴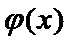
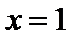
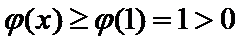
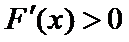
∴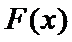
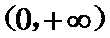
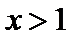
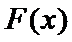
故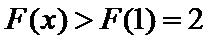
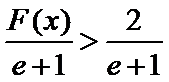
令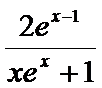
∵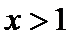
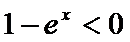
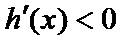
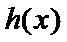
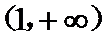
∴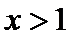
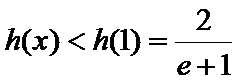
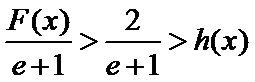
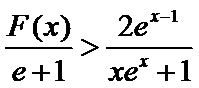
所以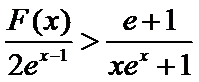
考查方向
解题思路
(1)先对函数进行求导,再对参数进行分类讨论探讨函数的单调性从而研究其最小值及此时a的值 ;(2)通过灵活变形构造新函数的方法证明不等式。
易错点
对参数的分类讨论研究函数的最值。
12. 定义在




正确答案
解析
由奇函数




(1)当






(2)当




(3)当

①当



②当



③当





综上可知,

考查方向
解题思路
1.先利用奇函数求出函数在对称的区间上的单调性;
2.根据x的范围不同分类求出x的解后取并集。
易错点
1.不会奇函数在对称的区间上单调性相同这个结论;
2.分类讨论时不全或重复。
知识点
已知函数
27. 判断函数

28. 若

29.求证:
正确答案
(1)
解析
(Ⅰ)


考查方向
解题思路
直接求导后判断出
易错点
导后的函数不会变形为
正确答案
3;
解析
(Ⅱ)


令

又



当


∴

考查方向
解题思路
先分离参数后变为

易错点
无
正确答案
(3)略
解析
(Ⅲ)由(Ⅱ)知

令
∴
∴
考查方向
解题思路
根据第(2)问放缩
易错点
不会利用放缩法得到
2.关于x的不等式:
正确答案
–1<x<2
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析