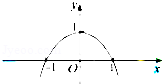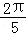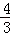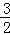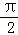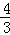- 相等向量与相反向量
- 共85题
在平面直角坐标系中,以坐标原点为极点,






(1)求

(2)圆c的参数方程为


正确答案
(1) 
解析
(1)由点

所以直线
从而直线
(2)由已知得圆
所以圆心为
以为圆心到直线的距离
知识点
平面直角坐标系xOy中,过椭圆M:


(1)求M的方程;
(2)C,D为M上两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值。
正确答案
(1) 
解析
(1)设A(x1,y1),B(x2,y2),P(x0,y0),
则


由此可得
因为x1+x2=2x0,y1+y2=2y0,
所以a2=2b2.
又由题意知,M的右焦点为(
因此a2=6,b2=3.
所以M的方程为
(2)由
解得
因此|AB|=
由题意可设直线CD的方程为
y=
设C(x3,y3),D(x4,y4)。
由
于是x3,4=
因为直线CD的斜率为1,
所以|CD|=
由已知,四边形ACBD的面积
当n=0时,S取得最大值,最大值为
所以四边形ACBD面积的最大值为
知识点
如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF=



(1)求二面角
(2)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使C
与
正确答案
见解析
解析
(1)
取线段EF的中点H,连结
因为
所以
又因为平面

所以
如图建立空间直角坐标系
则
故
设

所以
取
又平面BEF的一个法向量
故
所以二面角的余弦值为
(2)解:设
因为翻折后,C与A重合,所以CM=
故
经检验,此时点N在线段BG上,所以
方法二:
(1)解:
取截段EF的中点H,AF的中点G,连结
因为

又因为平面



又
故
又因为G,H是AF,EF的中点,
易知GH//AB,
所以GH
于是

所以

在
所以
故二面角

(2)解:设
因为翻折后,G与

而

经检验,此时点N在线段BC上,所以
知识点
已知二次函数y=f(x)的图象如图所示,则它与X轴所围图形的面积为 ( )
正确答案
解析
根据函数的图象可知二次函数y=f(x)图象过点(﹣1,0),(1,0),(0,1)
从而可知二次函数y=f(x)=﹣x2+1
∴它与X轴所围图形的面积为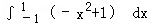
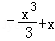
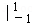
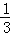
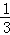
故选B。
知识点
若
正确答案
3
解析
略
知识点
扫码查看完整答案与解析