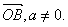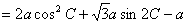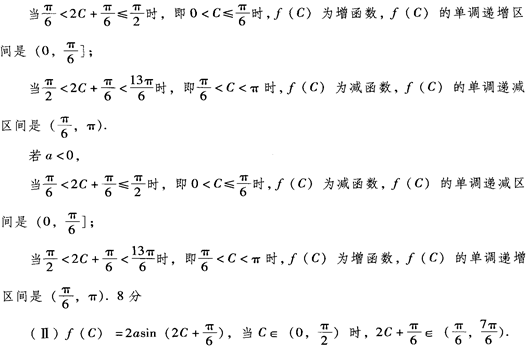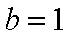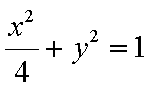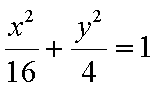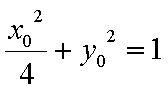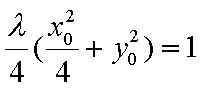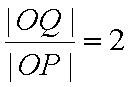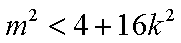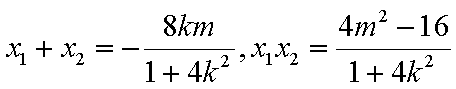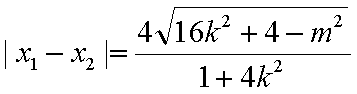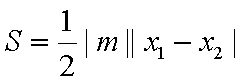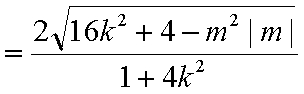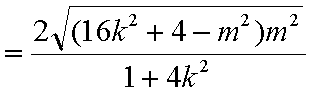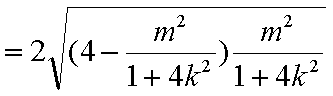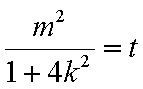- 相等向量与相反向量
- 共85题
已知函数

(1)求
(2)求
(3)若


正确答案
见解析。
解析
(1)
(2)由

又

∵


∴
(3)由(2)得
即

∵
∴
∴
知识点
如图,直角梯形ABCD中,∠DAB=90°,AD//BC,AB=2,

(1)建立适当的直角坐标系,求椭圆的方程;
(2)若点E满足
与椭圆F交于MN两点,且|ME|=|NE|,若存在,求K的取值
范围;若不存在,说明理由。
正确答案
见解析。
解析
.
(1)以AB中点为原点O,AB所在直线为x轴,建立直角坐标系,如图
则A(-1, 0), B(1, 0),D
设椭圆F的方程为
得
得4a4-17a2+4=0,∵a2>1,∴a2=4,b2=3.
所求椭圆F方程
(2)由
显然l⊥AB时不合条件,设l方程y=kx+m(k≠0)
代入
即4k2-m2+3>0
设M(x1,y1),N(x2,y2)中点为P(x0,y0)
|ME|=|NE|等价于PE⊥MN

PE⊥MN,得
得
代入△>0得

又∵k≠0故k取值范围为k∈
解法二:设M(x1,y1),N(x2,y2)
得
①一②得

设MN中点为P(x0,y0),得

|ME|=|NE|即PE⊥MN
得

又∵k≠0 ∴k取值范围为
知识点
在△ABC中,向量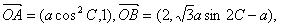
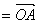
(1)求函数f(C)解析式,并求f(C)的单调区间;
(2)若△ABC是锐角三角形时,当a>O时,f(C)的最大值为5,求a的值。
正确答案
见解析。
解析
(1) f(C)
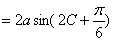
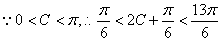
若a>O,
知识点
平面直角坐标系


(1)求圆
(2)若直线





(3)设











正确答案
见解析。
解析
(1)因为


所以圆

故圆

(2)设直线


由直线




当且仅当


(3)设




直线



直线



故
知识点
20.
平面直角坐标
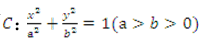
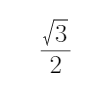
(1)求椭圆C的方程;
(2)设椭圆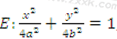
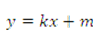
(i)求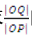
(ii)求△
正确答案
解:
(1)由题意知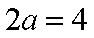

又
可得
所以椭圆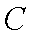
(2)由(1)知椭圆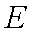
(i)设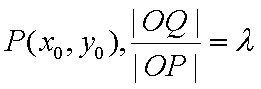
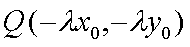
因为
又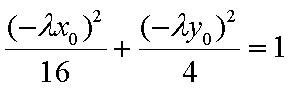
所以 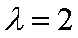
(ii)设
将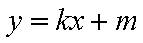
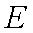
可得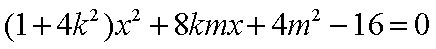
由 
则有
所以
因为 直线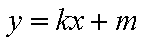
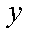
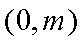
所以 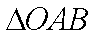
令
将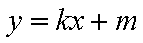
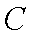
可得 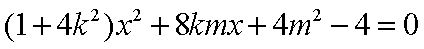
由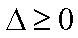
由①②可知 
因此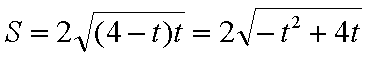
故 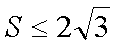
当且仅当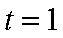

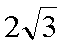
由(i)知,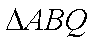
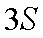
所以 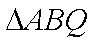
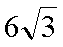
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析