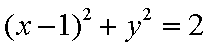- 圆的方程
- 共331题
12.在平面直角坐标系中,已知




正确答案
解析
设



∴
考查方向
解题思路
先设半圆曲线






易错点
正确设动点

知识点
12. 在平面直角坐标系中,已知




是____________
正确答案
解析
设


知识点


正确答案

解析
如图,


考查方向
解题思路
化为标准方程,
易错点
容易将方程的圆心坐标弄错,对图形的识别不准
知识点
12.已知直线



正确答案
解析
由已知得圆心到直线的距离小于半径,即
【或由
所以
由

如图,又由
因



考查方向
解题思路
1.先根据直线


易错点
不会转化题中向量的条件,导致无法做出正确答案。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种家和品种乙)进行田间试验,选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙。
(1)假设n=4,在第一大块地中,种植品种甲的小块地的数目记为X,求X的分布列和数学期望;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
附:样本数据x1,x2,…,xa的样本方差s2=




正确答案
见解析
解析
(1)由题意知X的可能取值是0,1,2,3,4,
P(X=0)=
P(X=1)=
P(X=2)=
P(X=3)=
P(X=4)=
∴X的分布列为
∴X的期望是
(2)品种甲的每公顷产量的样本平均数

方差是
品种乙每公顷的产量的样本平均数

方差是
有以上结果可以看出,品种乙的样本平均数大于品种甲的样本平均数,
且两个品种的样本方差差异不大,故应选择种植品种乙。
知识点
6. 圆x2+y2=4上与直线l:4x﹣3y+12=0距离最小的点的坐标是( )
正确答案
解析
过圆心O向直线4x-3y+12=0作垂线OP,与圆交于点P,则P点到直线距离最小.
∵OP垂直于直线4x-3y+12=0,∴斜率为-3/4
∴OP的方程为y=-3x/4
由y=-3x/4
x2+y2=4
得 x=-8/5 y=6/5
最小坐标(-8/5,6/5))
考查方向
直线与圆的关系
解题思路
1、首先要了解圆与直线的位置关系有哪些
2.直线和圆的位置关系的性质:
(1)直线l和⊙O相交<r
(2)直线l和⊙O相切d=r;
(3)直线l和⊙O相离d>r。
易错点
不熟悉直线与圆的位置关系以及性质。
教师点评
主要考查你对直线与圆的位置关系 等考点的理解。
知识点
如图,在平面直角坐标系xoy中,椭圆

26.求椭圆的方程;
27.若直线AB斜率为1时,求弦AB长;
28.过椭圆的对称中心O,作直线L,交椭圆与M,N,三角形FMN是否存在在大面积?若存在,求出它的最大面积值。若不存在,说明理由
正确答案
当AB的斜率为0时,AB=半长轴,即
2a=4,a=2;
又因为 e=c/a,
又
所以解析式为
解析
看解题步骤
考查方向
圆锥曲线
解题思路
利用离心率公式。abc之间的关系
易错点

教师点评
考查圆锥曲线解析式求解
正确答案
联立直线与椭圆方程得:5x2-8x=0设方程根为x1=0,x2=8/5,
|AB|=
解析
见答案
考查方向
直线与圆锥曲线的关系,两点之间的距离
解题思路
先求出两焦点的横坐标,利用距离与斜率、求两点间的距离公式求解
易错点
无
教师点评
考查了直线与圆锥曲线的关系,和用斜率求两点距离
正确答案
S⊿FMN= 

10.在平面直角坐标系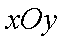
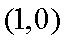
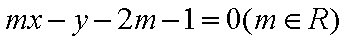
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,圆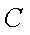
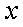
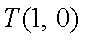
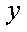
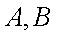
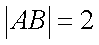
(1)圆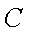
(2)过点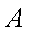
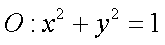
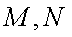
①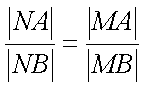
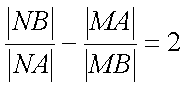
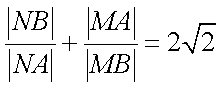
其中正确结论的序号是 _________. (写出所有正确结论的序号)
正确答案
(1)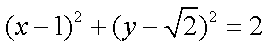
(2)①②③
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析